Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 51, 52 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Biểu đồ cột sau đây cho biết cỡ giày của các bạn nam khối 9 trong trường. Lập bảng tần số và tần số tương đối biểu diễn trên biểu đồ.
Đề bài
Biểu đồ cột sau đây cho biết cỡ giày của các bạn nam khối 9 trong trường.
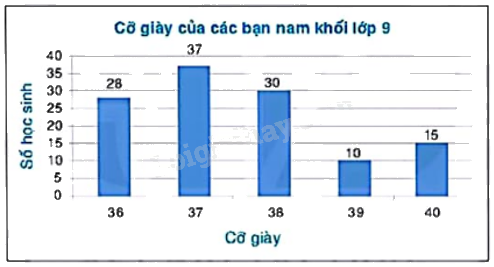
Lập bảng tần số và tần số tương đối biểu diễn trên biểu đồ.
Phương pháp giải - Xem chi tiết
- Cách lập bảng tần số:
+ Từ biểu đồ ta tìm được tần số tương ứng với cỡ giày \({x_i}\).
+ Lập bảng tần số có dạng:
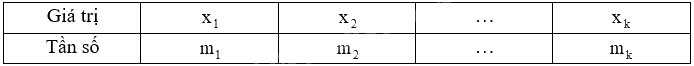
Trong bảng tần số, ta chỉ liệt kê các giá trị \({x_i}\) khác nhau, các giá trị \({x_i}\) này có thể không là số.
- Cách lập bảng tần số tương đối: + Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Giá trị \({x_i}\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối có dạng:
Giá trị | \({x_1}\) | … | \({x_k}\) |
Tần số tương đối | \({f_1}\) | … | \({f_k}\) |
Lời giải chi tiết
Tổng số học sinh nam khối 9 là: \(28 + 37 + 30 + 10 + 15 = 120\) (học sinh)
Số học sinh nam đi các cỡ giày 36, 37, 38, 39, 40 tương ứng là 28, 37, 30, 10, 15.
Ta có bảng tần số như sau:

Tỉ lệ học sinh nam đi các cỡ giày 36, 37, 38, 39, 40 tương ứng là: \(\frac{{28}}{{120}}.100\% \approx 23,33\% ;\frac{{37}}{{120}}.100\% \approx 30,83\% ;\frac{{30}}{{120}}.100\% = 25\% ;\frac{{10}}{{120}}.100\% \approx 8,34\% ;\frac{{15}}{{120}}.100\% = 12,5\% \)
Ta có bảng tần số tương đối như sau:

Bài 4 trang 51, 52 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Bài 4 bao gồm các dạng bài tập sau:
Để giải bài 4 trang 51, 52 Vở thực hành Toán 9 tập 2, học sinh cần nắm vững các kiến thức sau:
Dưới đây là hướng dẫn giải chi tiết từng phần của bài 4:
Để xác định hàm số bậc nhất, học sinh cần kiểm tra xem phương trình đã cho có dạng y = ax + b hay không. Nếu có, thì a và b là các hệ số của hàm số bậc nhất.
Để vẽ đồ thị hàm số bậc nhất, học sinh cần chọn hai điểm thuộc đồ thị và nối chúng lại với nhau. Hai điểm này có thể được chọn bằng cách thay các giá trị khác nhau của x vào phương trình hàm số và tính giá trị tương ứng của y.
Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình gồm phương trình của hai đường thẳng. Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Để ứng dụng hàm số bậc nhất vào giải quyết bài toán thực tế, học sinh cần xác định được các yếu tố liên quan đến bài toán và biểu diễn chúng bằng các biến số. Sau đó, học sinh cần xây dựng phương trình hàm số bậc nhất mô tả mối quan hệ giữa các biến số này và giải phương trình để tìm ra đáp án.
Ví dụ 1: Cho hàm số y = 2x + 1. Hãy xác định hệ số a và b của hàm số.
Giải: Hàm số y = 2x + 1 là hàm số bậc nhất với a = 2 và b = 1.
Ví dụ 2: Vẽ đồ thị của hàm số y = -x + 2.
Giải: Để vẽ đồ thị của hàm số y = -x + 2, ta chọn hai điểm thuộc đồ thị. Ví dụ, ta chọn x = 0 thì y = 2, và chọn x = 1 thì y = 1. Nối hai điểm (0, 2) và (1, 1) lại với nhau, ta được đồ thị của hàm số y = -x + 2.
Để củng cố kiến thức về hàm số bậc nhất, học sinh có thể luyện tập thêm các bài tập tương tự trong sách giáo khoa và sách bài tập. Ngoài ra, học sinh cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán.
Bài 4 trang 51, 52 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ giải quyết bài tập một cách dễ dàng và hiệu quả.