Bài 5 trang 52, 53 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán.
Cho biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh khối lớp 9 tại một trường Trung học cơ sở theo mức độ béo – gầy dựa vào chỉ số BMI. a) Lập bảng tần số tương đối cho dữ liệu trên biểu đồ. b) Giả sử trường Trung học cơ sở này có 800 học sinh. Tìm số học sinh theo mỗi mức phân loại.
Đề bài
Cho biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh khối lớp 9 tại một trường Trung học cơ sở theo mức độ béo – gầy dựa vào chỉ số BMI.
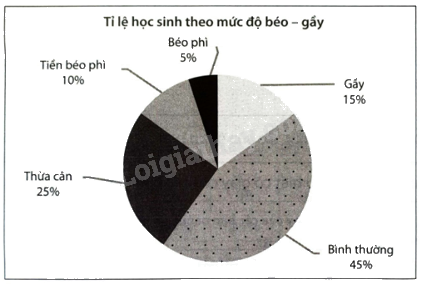
a) Lập bảng tần số tương đối cho dữ liệu trên biểu đồ.
b) Giả sử trường Trung học cơ sở này có 800 học sinh. Tìm số học sinh theo mỗi mức phân loại.
Phương pháp giải - Xem chi tiết
a) + Lập bảng tần số tương đối:
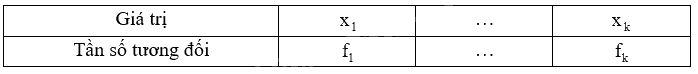
Trong đó \({f_i}\) là tần số tương đối của giá trị \({x_1}\).
b) Số học sinh theo mỗi mức phân loại bằng 800. tỉ lệ học sinh tương ứng với mức phân loại đó.
Lời giải chi tiết
a) Bảng tần số tương đối:

b) Số học sinh gầy là: \(800.15\% = 120\) (học sinh)
Số học sinh bình thường là: \(800.45\% = 360\) (học sinh)
Số học sinh thừa cân là: \(800.25\% = 200\) (học sinh)
Số học sinh tiền béo phì là: \(800.10\% = 80\) (học sinh)
Số học sinh béo phì là: \(800.5\% = 40\) (học sinh)
Bài 5 trong Vở thực hành Toán 9 tập 2 thường xoay quanh việc xác định hệ số góc và tung độ gốc của đường thẳng, hoặc tìm điều kiện để đường thẳng song song, vuông góc, cắt nhau. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất và hàm số bậc hai, cũng như các công thức liên quan.
Bài 5 thường được chia thành các phần nhỏ, yêu cầu học sinh thực hiện các thao tác khác nhau. Ví dụ:
Để minh họa, chúng ta sẽ xem xét một ví dụ cụ thể. Giả sử bài toán yêu cầu tìm giá trị của m để đường thẳng y = (m-1)x + 2 song song với đường thẳng y = 2x - 1.
Lời giải:
Để hai đường thẳng song song, hệ số góc của chúng phải bằng nhau và tung độ gốc phải khác nhau. Do đó, ta có:
m - 1 = 2
=> m = 3
Vậy, với m = 3, đường thẳng y = (m-1)x + 2 song song với đường thẳng y = 2x - 1.
Ngoài dạng bài tập tìm điều kiện song song, vuông góc, bài 5 còn có thể xuất hiện các dạng bài tập khác như:
Đối với mỗi dạng bài tập, học sinh cần áp dụng các công thức và phương pháp giải phù hợp. Ví dụ, để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình tương ứng với hai đường thẳng đó.
Để nắm vững kiến thức và kỹ năng giải bài tập, học sinh nên luyện tập thường xuyên với các bài tập tương tự. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng, giúp các em củng cố kiến thức và tự tin hơn trong quá trình học tập.
Ngoài việc giải các bài tập trong Vở thực hành, học sinh có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất và hàm số bậc hai trong thực tế. Ví dụ, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa nhiệt độ và độ cao.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình đường thẳng |
| a1 * a2 = -1 | Điều kiện vuông góc |
| a1 = a2, b1 ≠ b2 | Điều kiện song song |
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài 5 trang 52, 53 Vở thực hành Toán 9 tập 2 và đạt kết quả tốt trong môn Toán.