Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 109 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như hình dưới đây. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
Đề bài
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như hình dưới đây. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?
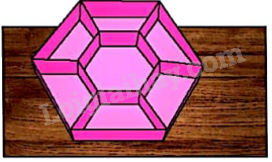
Phương pháp giải - Xem chi tiết
+ Nếu chia đôi lục giác đều nhỏ bởi một đường kính thì ra sẽ được hai hình thang cân nhỏ bằng nhau và bằng với các hình thang cân trước đó.
+ Do vậy đường kính của lục giác đều nhỏ phải bằng cạnh của lục giác đều lớn, từ đó tính được cạnh lục giác đều nhỏ.
Lời giải chi tiết
Nếu chia đôi lục giác đều nhỏ bởi một đường kính thì ra sẽ được hai hình thang cân nhỏ bằng nhau và bằng với các hình thang cân trước đó.
Do vậy đường kính của lục giác đều nhỏ phải bằng cạnh của lục giác đều lớn, tức là bằng 10 cm.
Vì vậy, cạnh lục giác đều nhỏ bằng \(\frac{1}{2}.10 = 5\) (cm).
Bài 6 trang 109 Vở thực hành Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như cách vẽ đồ thị hàm số.
Trước khi bắt đầu giải bài toán, hãy đọc kỹ đề bài và xác định rõ các thông tin đã cho và yêu cầu của bài toán. Chia bài toán thành các phần nhỏ hơn để dễ dàng tiếp cận và giải quyết. Ví dụ, nếu bài toán yêu cầu tìm phương trình đường thẳng đi qua hai điểm, bạn cần xác định tọa độ của hai điểm đó và áp dụng công thức tính phương trình đường thẳng.
Bài toán: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(-1; 0).
Giải:
Để giải nhanh các bài toán về hàm số, bạn nên thuộc lòng các công thức và phương pháp đã học. Luyện tập thường xuyên với các bài tập khác nhau để nắm vững kiến thức và rèn luyện kỹ năng giải toán. Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra lại kết quả.
Khi giải bài toán về hàm số, hãy chú ý đến đơn vị của các đại lượng. Kiểm tra lại kết quả trước khi kết luận để tránh sai sót. Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong Vở thực hành Toán 9 tập 2 hoặc trên các trang web học Toán online khác. Đừng ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn.
Bài 6 trang 109 Vở thực hành Toán 9 tập 2 là một bài toán quan trọng giúp học sinh hiểu rõ hơn về hàm số và ứng dụng của nó. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải đúng đắn và luyện tập thường xuyên, bạn có thể tự tin giải quyết bài toán này một cách hiệu quả.