Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 118 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng.
Đề bài
Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng.
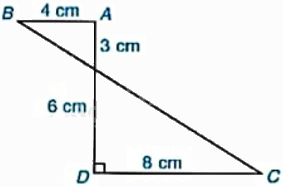
Phương pháp giải - Xem chi tiết
Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
Hình tạo thành là hai hình nón. Hình nón 1 có: \({R_1} = 8{\rm{\;cm}},{h_1} = 6{\rm{\;cm}}\); hình nón 2 có: \({R_2} = 4{\rm{\;cm}},{h_2} = 3{\rm{\;cm}}\).
Thể tích của hình nón 1 là: \({V_1} = \frac{1}{3}\pi R_1^2{h_1} = \frac{1}{3}\pi \cdot {8^2} \cdot 6 = 128\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích của hình nón 2 là: \({V_2} = \frac{1}{3}\pi {R_2}{\;^2}{h_2} = \frac{1}{3}\pi \cdot {4^2} \cdot 3 = 16\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích hình tạo thành là: \(V = {V_1} + {V_2} = 128\pi + 16\pi = 144\pi \,\,\;\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Bài 6 trang 118 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong quá trình ôn tập chương hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất, bao gồm:
Bài 6 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh giải bài tập này một cách hiệu quả, chúng tôi xin trình bày lời giải chi tiết như sau:
(a) Bài 6a: (Giả sử bài 6a yêu cầu xác định hệ số a của hàm số y = ax + b khi biết đồ thị đi qua hai điểm A(1; 2) và B(-1; 0)).
Để tìm hệ số a, ta thay tọa độ của hai điểm A và B vào phương trình hàm số y = ax + b:
Giải hệ phương trình (1) và (2), ta được:
Vậy, hàm số cần tìm là y = x + 1.
(b) Bài 6b: (Giả sử bài 6b yêu cầu tìm tọa độ giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2).
Để tìm tọa độ giao điểm, ta giải hệ phương trình:
Thay y = 2x - 1 vào phương trình thứ hai, ta được:
2x - 1 = -x + 2 => 3x = 3 => x = 1
Thay x = 1 vào phương trình y = 2x - 1, ta được:
y = 2 * 1 - 1 = 1
Vậy, tọa độ giao điểm của hai đường thẳng là (1; 1).
Để củng cố kiến thức về hàm số bậc nhất, các em có thể tham khảo thêm các bài tập tương tự sau:
Bài 6 trang 118 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp các em học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em sẽ tự tin giải bài tập này một cách hiệu quả.