Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 84, 85 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số, tập trung vào việc giải các bài toán liên quan đến hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Túi I đựng 4 quả cầu được đánh số 1, 2, 3, 4. Túi II đựng 5 quả cầu được đánh số 1, 2, 3, 4, 5. Lấy ngẫu nhiên một quả cầu từ mỗi túi I và II. a) Mô tả không gian mẫu. b) Tính xác suất của các biến cố sau: A: “Hai số ghi trên hai quả cầu bằng nhau”; B: “Hai số ghi trên hai quả cầu chênh nhau 2 đơn vị”; C: “Hai số ghi trên hai quả cầu chênh nhau lớn hơn 1 đơn vị”.
Đề bài
Túi I đựng 4 quả cầu được đánh số 1, 2, 3, 4. Túi II đựng 5 quả cầu được đánh số 1, 2, 3, 4, 5. Lấy ngẫu nhiên một quả cầu từ mỗi túi I và II.
a) Mô tả không gian mẫu.
b) Tính xác suất của các biến cố sau:
A: “Hai số ghi trên hai quả cầu bằng nhau”;
B: “Hai số ghi trên hai quả cầu chênh nhau 2 đơn vị”;
C: “Hai số ghi trên hai quả cầu chênh nhau lớn hơn 1 đơn vị”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
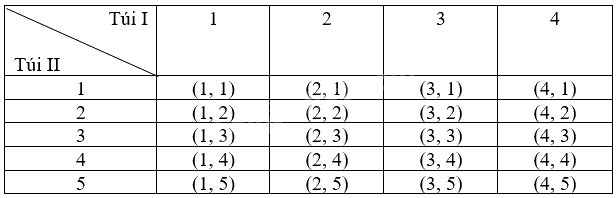
Mỗi ô ở bảng trên là một kết quả có thể. Có 20 kết quả có thể là đồng khả năng.
- Có 4 kết quả thuận lợi cho biến cố A là (1, 1); (2, 2); (3, 3); (4, 4). Vậy \(P\left( A \right) = \frac{4}{{20}} = \frac{1}{5}\).
- Có 6 kết quả thuận lợi cho biến cố B là (1, 3); (3, 1); (2; 4); (4; 2); (3, 5); (5, 3). Vậy \(P\left( B \right) = \frac{6}{{20}} = \frac{3}{{10}}\).
- Có 9 kết quả thuận lợi cho biến cố C là (1, 3); (1, 4); (1, 5); (2; 4); (2, 5); (3, 1); (3, 5); (4; 1); (4; 2). Vậy \(P\left( C \right) = \frac{9}{{20}}\).
Bài 4 trang 84, 85 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9, giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đồ thị hàm số và các phương pháp giải toán liên quan.
Bài 4 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 4 trang 84, 85 Vở thực hành Toán 9 tập 2, học sinh có thể áp dụng các phương pháp sau:
Bài 4a: Vẽ đồ thị hàm số y = 2x - 1.
Giải:
Bài 4b: Xác định xem điểm M(2; 3) có thuộc đồ thị hàm số y = 2x - 1 hay không.
Giải:
Thay tọa độ điểm M(2; 3) vào phương trình hàm số y = 2x - 1, ta có: 3 = 2 * 2 - 1 = 3. Vậy, điểm M(2; 3) thuộc đồ thị hàm số y = 2x - 1.
Để củng cố kiến thức về hàm số bậc nhất, học sinh có thể làm thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác.
Bài 4 trang 84, 85 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.