Chào mừng các em học sinh đến với bài giải bài 1 trang 84 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án chi tiết và lời giải dễ hiểu cho bài tập này, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh giải quyết các bài toán một cách hiệu quả nhất.
Một cuốn sách khổ (17 times 24cm), tức là chiều rộng 17cm, chiều dài 24cm. Gọi (alpha ) là góc giữa đường chéo và cạnh 17cm. Tính (sin alpha ,cos alpha ) (làm tròn đến chữ số thập phân thứ hai) và tính số đo (alpha ) (làm tròn đến độ).
Đề bài
Một cuốn sách khổ \(17 \times 24cm\), tức là chiều rộng 17cm, chiều dài 24cm. Gọi \(\alpha \) là góc giữa đường chéo và cạnh 17cm. Tính \(\sin \alpha ,\cos \alpha \) (làm tròn đến chữ số thập phân thứ hai) và tính số đo \(\alpha \) (làm tròn đến độ).
Phương pháp giải - Xem chi tiết
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết
Giả sử ABCD là hình ảnh một trang sách (H.4.23) với \(AB = 17cm,BC = 24cm\), khi đó \(\widehat {BAC} = \alpha \)
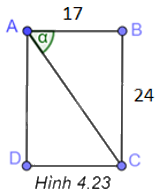
Trong tam giác vuông ABC, ta có
\(A{C^2} = A{B^2} + B{C^2} = {17^2} + {24^2} = 865\) nên \(AC = \sqrt {865} \)
Từ đó, \(\sin \alpha = \frac{{BC}}{{AC}} = \frac{{24}}{{\sqrt {865} }} \approx 0,82\); \(\cos \alpha = \frac{{AB}}{{AC}} = \frac{{17}}{{\sqrt {865} }} \approx 0,58\)
suy ra \(\alpha \approx {55^o}\).
Bài 1 trang 84 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để xác định hệ số góc, đường thẳng song song, và các tính chất liên quan đến hàm số.
Bài 1 trang 84 Vở thực hành Toán 9 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập.
Để xác định hệ số góc của một đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Hệ số góc a cho biết độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải. Nếu a = 0, đường thẳng là đường thẳng ngang.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song với nhau khi và chỉ khi a1 = a2 và b1 ≠ b2. Điều này có nghĩa là hai đường thẳng có cùng độ dốc nhưng khác nhau về vị trí trên trục tung.
Ba điểm A(x1, y1), B(x2, y2), và C(x3, y3) thẳng hàng khi và chỉ khi vectơ AB và vectơ AC cùng phương. Điều này có nghĩa là tỉ số giữa các tọa độ của hai vectơ này phải bằng nhau: (x2 - x1) / (x3 - x1) = (y2 - y1) / (y3 - y1).
Để lập phương trình đường thẳng khi biết hệ số góc a và một điểm A(x0, y0) thuộc đường thẳng, ta sử dụng công thức: y - y0 = a(x - x0). Công thức này cho phép ta xác định phương trình đường thẳng dựa trên độ dốc và một điểm cụ thể.
Giả sử chúng ta có đường thẳng y = 2x + 3. Hệ số góc của đường thẳng này là 2. Đường thẳng này đi lên từ trái sang phải.
Giả sử chúng ta có hai đường thẳng y = 3x + 1 và y = 3x + 2. Hai đường thẳng này song song với nhau vì chúng có cùng hệ số góc là 3.
Giả sử chúng ta có ba điểm A(1, 2), B(2, 4), và C(3, 6). Ba điểm này thẳng hàng vì (2 - 1) / (3 - 1) = (4 - 2) / (6 - 2) = 1.
Bài 1 trang 84 Vở thực hành Toán 9 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong quá trình giải bài tập và đạt kết quả tốt trong môn Toán.
Chúc các em học tập tốt!