Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 8 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số lớp 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho parabol (y = {x^2}) và đường thẳng d có phương trình (y = - 2x + 3). a) Vẽ parabol và đường thẳng trên cùng một hệ trục tọa độ Oxy. b) Từ đồ thị suy ra tọa độ các giao điểm A và B của đường thẳng và parabol.
Đề bài
Cho parabol \(y = {x^2}\) và đường thẳng d có phương trình \(y = - 2x + 3\).
a) Vẽ parabol và đường thẳng trên cùng một hệ trục tọa độ Oxy.
b) Từ đồ thị suy ra tọa độ các giao điểm A và B của đường thẳng và parabol.
Phương pháp giải - Xem chi tiết
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Cách vẽ đồ thị hàm số \(y = ax + b\): Biểu diễn tọa độ hai điểm thuộc đồ thị hàm số \(y = ax + b\). Nối hai điểm đó với nhau ta được đồ thị của hàm số \(y = ax + b\).
Lời giải chi tiết
a) HS tự vẽ các đồ thị.
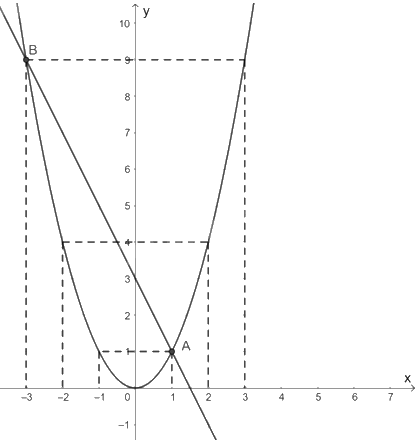
b) Từ đồ thị suy ra tọa độ của hai giao điểm là A(1; 1) và B(-3; 9).
Bài 7 trang 8 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập chương I về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và phân tích bài toán này:
Bài 7 yêu cầu học sinh thực hiện các nhiệm vụ sau:
a) Vẽ đồ thị của hàm số y = 2x - 3
Để vẽ đồ thị của hàm số y = 2x - 3, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = -3. Chọn x = 1, ta có y = -1. Vậy hai điểm A(0; -3) và B(1; -1) thuộc đồ thị hàm số.
Vẽ hệ trục tọa độ Oxy, đánh dấu hai điểm A(0; -3) và B(1; -1). Nối hai điểm này lại, ta được đồ thị của hàm số y = 2x - 3.
b) Xác định các điểm thuộc đồ thị hàm số
Để xác định một điểm thuộc đồ thị hàm số, ta chỉ cần thay giá trị x vào phương trình hàm số và tính giá trị y tương ứng. Ví dụ, nếu x = 2, thì y = 2(2) - 3 = 1. Vậy điểm C(2; 1) thuộc đồ thị hàm số.
c) Tìm giao điểm của đồ thị hàm số với trục hoành và trục tung
Giao điểm của đồ thị hàm số với trục hoành là điểm mà tại đó y = 0. Thay y = 0 vào phương trình hàm số, ta có 0 = 2x - 3, suy ra x = 3/2. Vậy giao điểm của đồ thị hàm số với trục hoành là điểm D(3/2; 0).
Giao điểm của đồ thị hàm số với trục tung là điểm mà tại đó x = 0. Thay x = 0 vào phương trình hàm số, ta có y = -3. Vậy giao điểm của đồ thị hàm số với trục tung là điểm A(0; -3).
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập sau:
Bài 7 trang 8 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và phân tích trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Lưu ý: Các em nên tự mình thực hiện các bước giải bài tập để hiểu rõ hơn về kiến thức và rèn luyện kỹ năng giải toán.
| Hàm số | Đồ thị | Giao điểm với trục hoành | Giao điểm với trục tung |
|---|---|---|---|
| y = 2x - 3 | Đường thẳng | (3/2; 0) | (0; -3) |