Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 82 Vở thực hành Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Có hai túi I và II. Túi I chứa 3 tấm thẻ, đánh số 2; 3; 4. Túi II chứa 2 tấm thẻ, đánh số 5; 6. Từ mỗi túi I và II, rút ngẫu nhiên một tấm thẻ. Tính xác suất của các biến cố sau: A: “Hai số ghi trên thẻ chênh lệch nhau 2 đơn vị”; B: “Hai số ghi trên thẻ chênh lệch nhau lớn hơn 2 đơn vị”; C: “Tích hai số ghi trên hai tấm thẻ là một số chẵn”; D: “Tổng hai số ghi trên hai tấm thẻ là một số nguyên tố”.
Đề bài
Có hai túi I và II. Túi I chứa 3 tấm thẻ, đánh số 2; 3; 4. Túi II chứa 2 tấm thẻ, đánh số 5; 6. Từ mỗi túi I và II, rút ngẫu nhiên một tấm thẻ. Tính xác suất của các biến cố sau:
A: “Hai số ghi trên thẻ chênh lệch nhau 2 đơn vị”;
B: “Hai số ghi trên thẻ chênh lệch nhau lớn hơn 2 đơn vị”;
C: “Tích hai số ghi trên hai tấm thẻ là một số chẵn”;
D: “Tổng hai số ghi trên hai tấm thẻ là một số nguyên tố”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Tập các kết quả có thể là tập cặp số (a, b) với \(a \in \left\{ {2;3;4} \right\};b \in \left\{ {5;6} \right\}.\)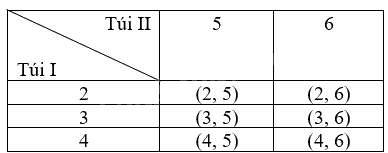
Mỗi ô ở bảng trên là một kết quả có thể. Không gian mẫu là \(\Omega = \left\{ {\left( {2,5} \right);\left( {2,6} \right);\left( {3,5} \right);\left( {3,6} \right);\left( {4,5} \right);\left( {4,6} \right)} \right\}\). Vậy có 6 kết quả có thể là đồng khả năng.
- Có 2 kết quả thuận lợi cho biến cố A là: (4, 6), (3, 5). Vậy \(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).
- Có 3 kết quả thuận lợi cho biến cố B là: (2, 5), (2, 6), (3, 6). Vậy \(P\left( B \right) = \frac{3}{6} = \frac{1}{2}\).
- Có 5 kết quả thuận lợi cho biến cố C là: (2, 5), (2, 6), (3, 6), (4, 5), (4, 6). Vậy \(P\left( C \right) = \frac{5}{6}\).
- Có 1 kết quả thuận lợi cho biến cố D là: (2, 5). Vậy \(P\left( D \right) = \frac{1}{6}\).
Bài 1 trang 82 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai đã được học để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị hàm số, và giải các phương trình, bất phương trình liên quan.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giúp các em hiểu rõ hơn về cách giải bài 1 trang 82, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu hỏi trong bài 1, giả sử bài 1 có 3 câu a, b, c)
Cho đường thẳng y = 2x - 3. Xác định hệ số góc của đường thẳng.
Lời giải:
Dựa vào công thức y = ax + b, ta thấy hệ số góc của đường thẳng là a = 2.
Cho hàm số y = -x + 1. Điểm A(1, 0) có thuộc đồ thị hàm số hay không?
Lời giải:
Thay x = 1 vào hàm số, ta được y = -1 + 1 = 0. Vậy điểm A(1, 0) thuộc đồ thị hàm số.
Giải phương trình 3x + 2 = 8.
Lời giải:
3x = 8 - 2
3x = 6
x = 2
Để giải tốt các bài tập về hàm số, các em cần lưu ý những điều sau:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải bài 1 trang 82 Vở thực hành Toán 9 tập 2 và các bài tập tương tự. Chúc các em học tập tốt!