Chào mừng các em học sinh đến với lời giải chi tiết bài 6 trang 87 Vở thực hành Toán 9. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.29a). Chiều rộng của mặt trên AB của đập là 3m. Độ dốc của sườn AD, tức là (tan D = 1,25). Độ dốc của sườn BC, tức là (tan C = 1,5). Chiều cao của đập là 3,5m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Đề bài
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.29a). Chiều rộng của mặt trên AB của đập là 3m. Độ dốc của sườn AD, tức là \(\tan D = 1,25\). Độ dốc của sườn BC, tức là \(\tan C = 1,5\). Chiều cao của đập là 3,5m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
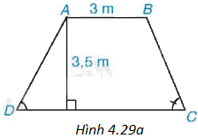
Phương pháp giải - Xem chi tiết
+ Kẻ các đường cao AH, BK của hình thang ABCD thì D, H, K, C nằm theo thứ tự đó trên đoạn DC.
+ Trong tam giác vuông AHD, ta có \(DH = \frac{{AH}}{{\tan D}}\), tính được DH.
+ Trong tam giác vuông BKC, ta có \(KC = \frac{{BK}}{{\tan C}}\), tính được KC.
+ Ta có: \(DC = DH + HK + KC\)
+ Áp dụng định lí Pythagore vào tam giác AHD vuông tại H tính được AD.
+ Áp dụng định lí Pythagore vào tam giác BKC vuông tại K tính được BC.
Lời giải chi tiết
(H.4.29b)
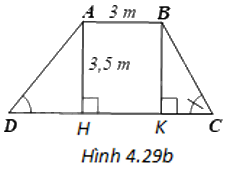
Kẻ các đường cao AH, BK của hình thang ABCD thì D, H, K, C nằm theo thứ tự đó trên đoạn DC.
Trong tam giác vuông AHD, ta có
\(DH = \frac{{AH}}{{\tan D}} = \frac{{3,5}}{{1,25}} = 2,8\)
Trong tam giác vuông BKC, ta có
\(KC = \frac{{BK}}{{\tan C}} = \frac{{3,5}}{{1,5}} \approx 2,3\)
Ta có:
\(DC = DH + HK + KC = 2,8 + 3 + 2,3 = 8,1\left( m \right)\)
Trong tam giác AHD, ta có
\(A{D^2} = A{H^2} + H{D^2} = {3,5^2} + {2,8^2}\),
suy ra \(AD \approx 4,5m\).
Trong tam giác vuông BKC, ta có
\(B{C^2} = B{K^2} + K{C^2} = {3,5^2} + {2,3^2}\), suy ra \(BC \approx 4,2m\).
Bài 6 trang 87 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 6 bao gồm các dạng bài tập sau:
Cho hàm số y = 2x - 3. Tìm y khi x = -1; x = 0; x = 2.
Lời giải:
Cho hàm số y = -x + 1. Tìm x khi y = 0; y = 2; y = -1.
Lời giải:
Tìm hệ số a của hàm số y = ax + 1, biết rằng khi x = 2 thì y = 5.
Lời giải:
Thay x = 2 và y = 5 vào hàm số y = ax + 1, ta có:
5 = a*2 + 1 => 2a = 4 => a = 2
Vậy, hệ số a = 2.
Tìm hệ số a của hàm số y = ax - 2, biết rằng khi x = -1 thì y = 3.
Lời giải:
Thay x = -1 và y = 3 vào hàm số y = ax - 2, ta có:
3 = a*(-1) - 2 => -a = 5 => a = -5
Vậy, hệ số a = -5.
Tìm hàm số y = ax + b, biết rằng đồ thị của hàm số đi qua hai điểm A(0; -2) và B(1; 1).
Lời giải:
Thay tọa độ điểm A(0; -2) vào hàm số y = ax + b, ta có:
-2 = a*0 + b => b = -2
Thay tọa độ điểm B(1; 1) và b = -2 vào hàm số y = ax + b, ta có:
1 = a*1 - 2 => a = 3
Vậy, hàm số cần tìm là y = 3x - 2.
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh đã có thể tự tin giải quyết bài 6 trang 87 Vở thực hành Toán 9 một cách hiệu quả. Chúc các em học tập tốt!