Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Chúng tôi giúp bạn giải quyết các câu hỏi trắc nghiệm trong Vở thực hành Toán 9 trang 101 một cách nhanh chóng và hiệu quả.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những lời giải chính xác và phương pháp giải bài tập tối ưu nhất.
Cho đường tròn (O) có bán kính bằng 12cm. Khi đó, dây lớn nhất của đường tròn (O; 12cm) có độ dài bằng A. 6cm. B. 36cm. C. 12cm. D. 24cm.
Trả lời Câu 1 trang 101 Vở thực hành Toán 9
Cho đường tròn (O) có bán kính bằng 12cm. Khi đó, dây lớn nhất của đường tròn (O; 12cm) có độ dài bằng
A. 6cm.
B. 36cm.
C. 12cm.
D. 24cm.
Phương pháp giải:
Trong một đường tròn, đường kính là dây lớn nhất.
Lời giải chi tiết:
Dây lớn nhất của đường tròn (O; 12cm) là đường kính nên dây lớn nhất có độ dài là: 2.12=24(cm)
Chọn D
Trả lời Câu 2 trang 101 Vở thực hành Toán 9
Cho đường tròn (O; R) và điểm M nằm trong đường tròn (O). Kẻ dây AB của đường tròn (O) nhận M làm trung điểm. Biết \(R = 5cm\) và \(OM = 1,4cm\). Độ dài dây AB là
A. 9,5cm.
B. 9,6cm.
C. 9,8cm.
D. 9cm.
Phương pháp giải:
+ Chứng minh tam giác AOB cân tại O, suy ra OM là đường trung tuyến đồng thời là đường cao.
+ Áp dụng định lí Pythagore vào tam giác OMB vuông tại M ta tính được MB.
+ \(AB = 2MB\).
Lời giải chi tiết:
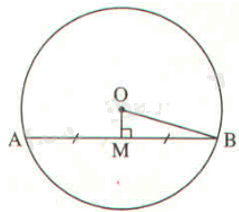
Tam giác AOB có \(OA = OB\) (bán kính (O)) nên tam giác AOB cân tại O. Do đó, OM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác OMB vuông tại M có: \(M{B^2} + O{M^2} = O{B^2}\)
Suy ra \(MB = \sqrt {O{B^2} - O{M^2}} = \sqrt {{5^2} - {{1,4}^2}} = 4,8\left( {cm} \right)\)
Do đó, \(AB = 2MB = 2.4,8 = 9,6\left( {cm} \right)\)
Chọn B
Trả lời Câu 3 trang 101 Vở thực hành Toán 9
Cho Hình 5.7. Khẳng định nào sau đây là đúng?
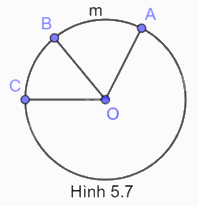
A. Cung AmB bị chắn bởi góc ở tâm AOB.
B. Góc ở tâm AOC chắn cung AB.
C. Cung AmB bị chắn bởi góc ở tâm BOC.
D. Góc ở tâm AOC chắn cung BC.
Phương pháp giải:
Quan sát hình và rút ra kết luận.
Lời giải chi tiết:
Cung AmB bị chắn bởi góc ở tâm AOB.
Chọn A
Trả lời Câu 4 trang 101 Vở thực hành Toán 9
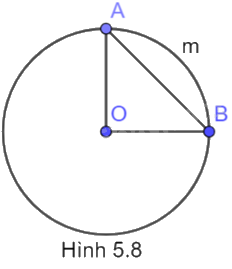
Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là
A. \({45^o}\).
B. \({90^o}\).
C. \({270^o}\).
D. \({60^o}\).
Phương pháp giải:
Trong một đường tròn, số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết:
Vì A, B thuộc (O) nên \(OA = OB = R\)
Ta có: \(A{B^2} = O{A^2} + O{B^2}\) nên tam giác OAB vuông tại O. Do đó, \(\widehat {AOB} = {90^o}\)
Vì góc ở tâm AOB chắn cung AmB nên \(sđ\overset\frown{AmB}=\widehat{AOB}={{90}^{o}}\)
Chọn B
Chọn phương án đúng cho mỗi câu sau:
Trả lời Câu 1 trang 101 Vở thực hành Toán 9
Cho đường tròn (O) có bán kính bằng 12cm. Khi đó, dây lớn nhất của đường tròn (O; 12cm) có độ dài bằng
A. 6cm.
B. 36cm.
C. 12cm.
D. 24cm.
Phương pháp giải:
Trong một đường tròn, đường kính là dây lớn nhất.
Lời giải chi tiết:
Dây lớn nhất của đường tròn (O; 12cm) là đường kính nên dây lớn nhất có độ dài là: 2.12=24(cm)
Chọn D
Trả lời Câu 2 trang 101 Vở thực hành Toán 9
Cho đường tròn (O; R) và điểm M nằm trong đường tròn (O). Kẻ dây AB của đường tròn (O) nhận M làm trung điểm. Biết \(R = 5cm\) và \(OM = 1,4cm\). Độ dài dây AB là
A. 9,5cm.
B. 9,6cm.
C. 9,8cm.
D. 9cm.
Phương pháp giải:
+ Chứng minh tam giác AOB cân tại O, suy ra OM là đường trung tuyến đồng thời là đường cao.
+ Áp dụng định lí Pythagore vào tam giác OMB vuông tại M ta tính được MB.
+ \(AB = 2MB\).
Lời giải chi tiết:
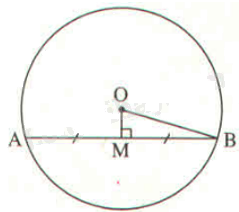
Tam giác AOB có \(OA = OB\) (bán kính (O)) nên tam giác AOB cân tại O. Do đó, OM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác OMB vuông tại M có: \(M{B^2} + O{M^2} = O{B^2}\)
Suy ra \(MB = \sqrt {O{B^2} - O{M^2}} = \sqrt {{5^2} - {{1,4}^2}} = 4,8\left( {cm} \right)\)
Do đó, \(AB = 2MB = 2.4,8 = 9,6\left( {cm} \right)\)
Chọn B
Trả lời Câu 3 trang 101 Vở thực hành Toán 9
Cho Hình 5.7. Khẳng định nào sau đây là đúng?
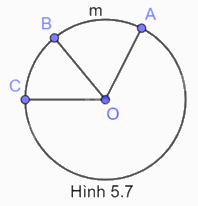
A. Cung AmB bị chắn bởi góc ở tâm AOB.
B. Góc ở tâm AOC chắn cung AB.
C. Cung AmB bị chắn bởi góc ở tâm BOC.
D. Góc ở tâm AOC chắn cung BC.
Phương pháp giải:
Quan sát hình và rút ra kết luận.
Lời giải chi tiết:
Cung AmB bị chắn bởi góc ở tâm AOB.
Chọn A
Trả lời Câu 4 trang 101 Vở thực hành Toán 9
Cho đường tròn (O; R), vẽ dây \(AB = \sqrt 2 R\) (H.5.8). Số đo của cung AmB là
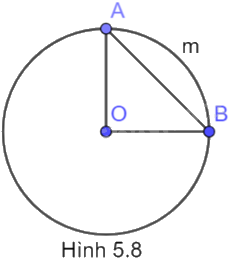
A. \({45^o}\).
B. \({90^o}\).
C. \({270^o}\).
D. \({60^o}\).
Phương pháp giải:
Trong một đường tròn, số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Lời giải chi tiết:
Vì A, B thuộc (O) nên \(OA = OB = R\)
Ta có: \(A{B^2} = O{A^2} + O{B^2}\) nên tam giác OAB vuông tại O. Do đó, \(\widehat {AOB} = {90^o}\)
Vì góc ở tâm AOB chắn cung AmB nên \(sđ\overset\frown{AmB}=\widehat{AOB}={{90}^{o}}\)
Chọn B
Trang 101 Vở thực hành Toán 9 thường chứa các bài tập trắc nghiệm liên quan đến một chủ đề cụ thể đã được học. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là yếu tố then chốt để đạt kết quả tốt. Bài viết này sẽ cung cấp lời giải chi tiết cho từng câu hỏi trắc nghiệm, đồng thời phân tích phương pháp giải và những lưu ý quan trọng.
Thông thường, trang 101 Vở thực hành Toán 9 sẽ tập trung vào một trong các chủ đề sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trắc nghiệm trang 101 Vở thực hành Toán 9. (Lưu ý: Vì không có nội dung cụ thể của trang 101, chúng ta sẽ đưa ra ví dụ minh họa)
Câu hỏi: Phương trình 2x + 3 = 0 có nghiệm là?
A. x = -3/2
B. x = 3/2
C. x = 2
D. x = -2
Lời giải:
2x + 3 = 0
2x = -3
x = -3/2
Đáp án: A
Câu hỏi: Cho đường tròn (O; 5cm) và một điểm A sao cho OA = 3cm. Khi đó, điểm A nằm…
A. Nằm ngoài đường tròn
B. Nằm trên đường tròn
C. Nằm trong đường tròn
D. Không xác định
Lời giải:
Vì OA < R (3cm < 5cm) nên điểm A nằm trong đường tròn.
Đáp án: C
Để giải bài tập trắc nghiệm Toán 9 hiệu quả, bạn nên:
Việc luyện tập thường xuyên là yếu tố quan trọng để nắm vững kiến thức và kỹ năng giải bài tập. Bạn có thể tìm các bài tập trắc nghiệm trên sách giáo khoa, vở bài tập, các trang web học toán online hoặc tham gia các khóa học luyện thi.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và phương pháp giải bài tập trắc nghiệm trang 101 Vở thực hành Toán 9 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!