Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 123, 124 Vở thực hành Toán 9 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
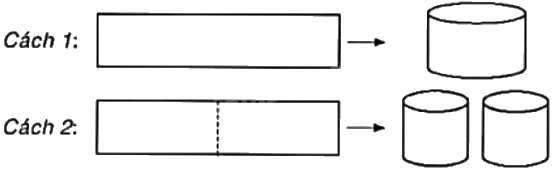
Từ một tấm tôn hình chữ nhật có kích thước (50cm times 240cm), người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau: • Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ. • Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu ({V_1}) là thể tích của thùng gò được theo Cách 1 và ({V_2}) là tổng thể tích của hai thùng gò được theo Cách 2. Tính tỉ số (frac{{{V_
Đề bài
Từ một tấm tôn hình chữ nhật có kích thước \(50cm \times 240cm\), người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau:
Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng nước hình trụ.
Cách 2: Cắt tấm tôn ban đầu thành hai tấm bằng nhau hình chữ nhật, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu \({V_1}\) là thể tích của thùng gò được theo Cách 1và \({V_2}\) là tổng thể tích của hai thùng gò được theo Cách 2. Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) (giả sử các mối hàn là không đáng kể).
Phương pháp giải - Xem chi tiết
+ Nếu làm theo cách 1 thì chu vi đường tròn đáy là: 240cm; \({R_1} = \frac{{240}}{{2\pi }}\).
+ Nếu làm theo cách 2 thì chu vi đường tròn đáy bằng 120cm, \({R_2} = \frac{{120}}{{2\pi }}\).
+ Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
Lời giải chi tiết
Nếu làm theo cách 1 thì chu vi đường tròn đáy là: 240cm; \({R_1} = \frac{{240}}{{2\pi }} = \frac{{120}}{\pi }\left( {cm} \right)\).
Nếu làm theo cách 2 thì chu vi của mỗi đường tròn đáy bằng 120cm, \({R_2} = \frac{{120}}{{2\pi }} = \frac{{60}}{\pi }\left( {cm} \right)\).
Ta có: \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\pi R_1^2h}}{{2\pi R_2^2h}}= \frac{{R_1^2}}{{2R_2^2}} = \frac{1}{2}{\left( {\frac{{{R_1}}}{{{R_2}}}} \right)^2}\)
\(= \frac{1}{2} \cdot {\left( {\frac{{120}}{\pi }:\frac{{60}}{\pi }} \right)^2} = 2\).
Bài 6 trong Vở thực hành Toán 9 tập 2 thường tập trung vào các chủ đề như phương trình bậc hai một ẩn, hệ phương trình bậc hai hai ẩn, hoặc các bài toán liên quan đến hàm số bậc hai. Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về các chủ đề này, bao gồm cách giải phương trình, cách giải hệ phương trình, và cách xác định các yếu tố của hàm số bậc hai.
Bài 6 trang 123 thường là một bài toán về phương trình bậc hai. Để giải bài toán này, bạn có thể sử dụng các phương pháp sau:
Ví dụ: Giải phương trình x^2 - 5x + 6 = 0
Ta có thể phân tích phương trình thành (x - 2)(x - 3) = 0. Vậy nghiệm của phương trình là x = 2 và x = 3.
Bài 6 trang 124 có thể là một bài toán về hệ phương trình bậc hai hai ẩn. Để giải bài toán này, bạn có thể sử dụng các phương pháp sau:
Ví dụ: Giải hệ phương trình sau:
x + y = 5
x - y = 1
Cộng hai phương trình, ta được 2x = 6, suy ra x = 3. Thay x = 3 vào phương trình x + y = 5, ta được y = 2. Vậy nghiệm của hệ phương trình là x = 3 và y = 2.
Việc giải bài 6 trang 123, 124 Vở thực hành Toán 9 tập 2 đòi hỏi bạn phải nắm vững các kiến thức cơ bản về phương trình bậc hai và hệ phương trình bậc hai. Bằng cách áp dụng các phương pháp giải phù hợp và kiểm tra lại kết quả, bạn có thể giải bài tập này một cách hiệu quả. Chúc bạn học tốt!
| Chủ đề | Phương pháp giải |
|---|---|
| Phương trình bậc hai | Phân tích thành nhân tử, công thức nghiệm, hoàn thiện bình phương |
| Hệ phương trình bậc hai | Phương pháp thế, phương pháp cộng đại số |