Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này tập trung vào việc giải các câu hỏi trắc nghiệm trang 122 Vở thực hành Toán 9, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các giải thích rõ ràng để bạn có thể hiểu được bản chất của vấn đề.
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết (OA = sqrt {15} cm) và (OB = 4cm). Khi đó: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm ngoài (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm trong (O), điểm B nằm trên (O).
Trả lời Câu 1 trang 122 Vở thực hành Toán 9
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết \(OA = \sqrt {15} cm\) và \(OB = 4cm\). Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Phương pháp giải:
+ Điểm M nằm trên đường tròn (O; R) nếu \(OM = R\).
+ Điểm M nằm trong đường tròn (O; R) nếu \(OM < R\).
+ Điểm M nằm ngoài đường tròn (O; R) nếu \(OM > R\).
Lời giải chi tiết:
Vì \(OA < 4cm\) nên điểm A nằm trong (O) và \(OB = 4cm\) nên điểm B nằm trên (O).
Chọn D
Trả lời Câu 2 trang 122 Vở thực hành Toán 9
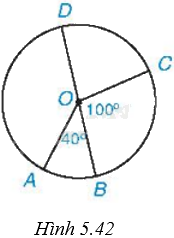
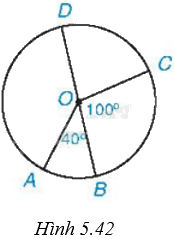
Cho Hình 5.42, trong đó BD là đường kính, \(\widehat {AOB} = {40^o};\widehat {BOC} = {100^o}\). Khi đó:
A. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
B. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
C. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
D. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
Phương pháp giải:
Trong một đường tròn, số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó.
Lời giải chi tiết:
Ta có: \(\widehat {BOC} + \widehat {DOC} = {180^o}\) nên \(\widehat {DOC} = {180^o} - \widehat {BOC} = {180^o} - {100^o} = {80^o}\).
\(\widehat {BOA} + \widehat {DOA} = {180^o}\) nên \(\widehat {DOA} = {180^o} - \widehat {BOA} = {180^o} - {40^o} = {140^o}\).
Vì góc ở tâm DOA chắn cung nhỏ AD nên \(sđ\overset\frown{AD}=\widehat{DOA}={{140}^{o}}\).
Vì góc ở tâm DOC chắn cung nhỏ DC nên \(sđ\overset\frown{DC}=\widehat{DOC}={{80}^{o}}\).
Chọn D
Trả lời Câu 4 trang 122 Vở thực hành Toán 9
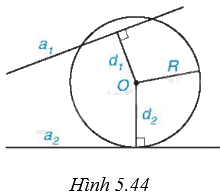
Cho đường tròn (O; R) và hai đường thẳng \({a_1}\) và \({a_2}\). Gọi \({d_1},{d_2}\) lần lượt là khoảng cách từ điểm O đến \({a_1}\) và \({a_2}\). Biết rằng (O) cắt \({a_1}\) và tiếp xúc với \({a_2}\) (H.5.44). Khi đó:
A. \({d_1} < R\) và \({d_2} = R\).
B. \({d_1} = R\) và \({d_2} < R\).
C. \({d_1} > R\) và \({d_2} = R\).
D. \({d_1} < R\) và \({d_2} < R\).
Phương pháp giải:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết:
Vì (O) cắt \({a_1}\) nên \({d_1} < R\). Vì (O) tiếp xúc với \({a_2}\) nên \({d_2} = R\).
Chọn A
Trả lời Câu 3 trang 122 Vở thực hành Toán 9
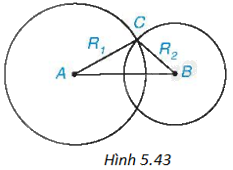
Cho hai đường tròn \(\left( {A;{R_1}} \right),\left( {B;{R_2}} \right)\), trong đó \({R_2} < {R_1}\). Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.43). Khi đó:
A. \(AB < {R_1} - {R_2}\).
B. \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
C. \(AB > {R_1} + {R_2}\).
D. \(AB = {R_1} + {R_2}\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) (với \(R > r\)) cắt nhau khi \(R - r < OO' < R + r\).
Lời giải chi tiết:
Vì hai đường tròn (A) và (B) cắt nhau nên \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
Chọn B
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 122 Vở thực hành Toán 9
Cho đường tròn (O; 4cm) và hai điểm A, B. Biết \(OA = \sqrt {15} cm\) và \(OB = 4cm\). Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Phương pháp giải:
+ Điểm M nằm trên đường tròn (O; R) nếu \(OM = R\).
+ Điểm M nằm trong đường tròn (O; R) nếu \(OM < R\).
+ Điểm M nằm ngoài đường tròn (O; R) nếu \(OM > R\).
Lời giải chi tiết:
Vì \(OA < 4cm\) nên điểm A nằm trong (O) và \(OB = 4cm\) nên điểm B nằm trên (O).
Chọn D
Trả lời Câu 2 trang 122 Vở thực hành Toán 9
Cho Hình 5.42, trong đó BD là đường kính, \(\widehat {AOB} = {40^o};\widehat {BOC} = {100^o}\). Khi đó:
A. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
B. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{220}^{o}}\).
C. \(sđ\overset\frown{DC}={{280}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
D. \(sđ\overset\frown{DC}={{80}^{o}}\) và \(sđ\overset\frown{AD}={{140}^{o}}\).
Phương pháp giải:
Trong một đường tròn, số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó.
Lời giải chi tiết:
Ta có: \(\widehat {BOC} + \widehat {DOC} = {180^o}\) nên \(\widehat {DOC} = {180^o} - \widehat {BOC} = {180^o} - {100^o} = {80^o}\).
\(\widehat {BOA} + \widehat {DOA} = {180^o}\) nên \(\widehat {DOA} = {180^o} - \widehat {BOA} = {180^o} - {40^o} = {140^o}\).
Vì góc ở tâm DOA chắn cung nhỏ AD nên \(sđ\overset\frown{AD}=\widehat{DOA}={{140}^{o}}\).
Vì góc ở tâm DOC chắn cung nhỏ DC nên \(sđ\overset\frown{DC}=\widehat{DOC}={{80}^{o}}\).
Chọn D
Trả lời Câu 3 trang 122 Vở thực hành Toán 9
Cho hai đường tròn \(\left( {A;{R_1}} \right),\left( {B;{R_2}} \right)\), trong đó \({R_2} < {R_1}\). Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.43). Khi đó:
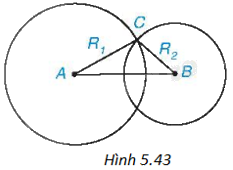
A. \(AB < {R_1} - {R_2}\).
B. \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
C. \(AB > {R_1} + {R_2}\).
D. \(AB = {R_1} + {R_2}\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) (với \(R > r\)) cắt nhau khi \(R - r < OO' < R + r\).
Lời giải chi tiết:
Vì hai đường tròn (A) và (B) cắt nhau nên \({R_1} - {R_2} < AB < {R_1} + {R_2}\).
Chọn B
Trả lời Câu 4 trang 122 Vở thực hành Toán 9
Cho đường tròn (O; R) và hai đường thẳng \({a_1}\) và \({a_2}\). Gọi \({d_1},{d_2}\) lần lượt là khoảng cách từ điểm O đến \({a_1}\) và \({a_2}\). Biết rằng (O) cắt \({a_1}\) và tiếp xúc với \({a_2}\) (H.5.44). Khi đó:
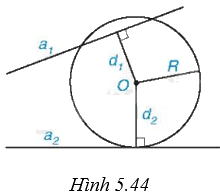
A. \({d_1} < R\) và \({d_2} = R\).
B. \({d_1} = R\) và \({d_2} < R\).
C. \({d_1} > R\) và \({d_2} = R\).
D. \({d_1} < R\) và \({d_2} < R\).
Phương pháp giải:
Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Khi đó:
+ Đường thẳng a và đường tròn (O; R) cắt nhau khi \(d < R\).
+ Đường thẳng a và đường tròn (O; R) tiếp xúc với nhau khi \(d = R\).
+ Đường thẳng a và đường tròn (O; R) không giao nhau khi \(d > R\).
Lời giải chi tiết:
Vì (O) cắt \({a_1}\) nên \({d_1} < R\). Vì (O) tiếp xúc với \({a_2}\) nên \({d_2} = R\).
Chọn A
Trang 122 Vở thực hành Toán 9 thường chứa các bài tập trắc nghiệm liên quan đến một chủ đề cụ thể đã được học. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt. Bài viết này sẽ đi sâu vào từng câu hỏi trắc nghiệm, cung cấp lời giải chi tiết và phân tích các phương pháp giải hiệu quả.
Để hiểu rõ hơn về nội dung của trang 122, chúng ta cần xác định chủ đề chính mà các câu hỏi trắc nghiệm tập trung vào. Thông thường, đây có thể là các chủ đề như:
Dưới đây là lời giải chi tiết cho từng câu hỏi trắc nghiệm trên trang 122 Vở thực hành Toán 9. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, kèm theo các giải thích chi tiết để bạn có thể hiểu được logic và phương pháp giải.
Đề bài: Cho phương trình x2 - 5x + 6 = 0. Nghiệm của phương trình là?
Lời giải:
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Để giải nhanh các bài tập trắc nghiệm Toán 9, bạn có thể áp dụng một số mẹo sau:
Việc giải các câu hỏi trắc nghiệm trang 122 Vở thực hành Toán 9 không chỉ giúp bạn ôn tập kiến thức mà còn rèn luyện kỹ năng giải bài tập trắc nghiệm. Đây là một kỹ năng rất quan trọng trong các kỳ thi như kiểm tra giữa học kỳ, kiểm tra cuối học kỳ và thi tuyển sinh vào lớp 10.
Để học Toán 9 hiệu quả hơn, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải các câu hỏi trắc nghiệm trang 122 Vở thực hành Toán 9 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!