Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 75 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em giải quyết mọi khó khăn trong môn Toán.
Cho tam giác ABC vuông tại A, biết (AB = 6cm,AC = 8cm). a) Tính tanB, cạnh BC, sinB, góc B (làm tròn đến độ). b) Kẻ đường cao AH. Tính AH, BH, cos (widehat {BAH}).
Đề bài
Cho tam giác ABC vuông tại A, biết \(AB = 6cm,AC = 8cm\).
a) Tính tanB, cạnh BC, sinB, góc B (làm tròn đến độ).
b) Kẻ đường cao AH. Tính AH, BH, cos \(\widehat {BAH}\).
Phương pháp giải - Xem chi tiết
a) + Tam giác ABC có: \(\tan B = \frac{{AC}}{{AB}}\).
+ Áp dụng Pythagore vào tam giác ABC tính được BC.
+ \(\sin B = \frac{{AC}}{{BC}}\)
b) Trong tam giác vuông ABH có:
+ \(\sin B = \frac{{AH}}{{AB}}\) từ đó tính được AH; \(\tan B = \frac{{AH}}{{BH}}\) từ đó tính được BH.
+ \(\cos \widehat {BAH} = \sin B = \frac{4}{5}\) (vì \(\widehat {BAH}\) và góc B là hai góc phụ nhau).
Lời giải chi tiết
(H.4.9)
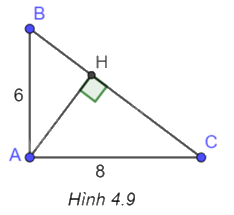
a) Trong tam giác ABC có \(\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}\).
Theo định lí Pythagore, ta có \(B{C^2} = A{C^2} + A{B^2} = {8^2} + {6^2} = 100\)
\(BC = \sqrt {100} = 10cm\)
Ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\), từ đó suy ra \(\widehat B \approx {53^o}\)
b) Trong tam giác vuông ABH có:
\(\sin B = \frac{{AH}}{{AB}}\), suy ra \(AH = AB.\sin B = 6.\frac{4}{5} = \frac{{24}}{5}\left( {cm} \right)\)
\(\tan B = \frac{{AH}}{{BH}}\), suy ra \(BH = \frac{{AH}}{{\tan B}} = \frac{{24}}{5}:\frac{4}{3} = \frac{{18}}{5}\left( {cm} \right)\)
\(\cos \widehat {BAH} = \sin B = \frac{4}{5}\) (vì \(\widehat {BAH}\) và góc B là hai góc phụ nhau).
Bài 8 trang 75 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 8 bao gồm các dạng bài tập sau:
Cho hàm số y = 2x - 3. Tìm x khi y = 5.
Giải:
Thay y = 5 vào hàm số y = 2x - 3, ta có:
5 = 2x - 3
2x = 8
x = 4
Vậy, khi y = 5 thì x = 4.
Xác định hệ số a của hàm số y = ax + 1 biết rằng đồ thị của hàm số đi qua điểm A(1; 3).
Giải:
Vì đồ thị của hàm số y = ax + 1 đi qua điểm A(1; 3) nên tọa độ của điểm A thỏa mãn phương trình của hàm số.
Thay x = 1 và y = 3 vào hàm số y = ax + 1, ta có:
3 = a(1) + 1
a = 2
Vậy, hệ số a của hàm số là 2.
Tìm đường thẳng đi qua hai điểm A(0; -2) và B(2; 0).
Giải:
Gọi phương trình đường thẳng cần tìm là y = ax + b.
Thay tọa độ điểm A(0; -2) vào phương trình, ta có:
-2 = a(0) + b
b = -2
Thay tọa độ điểm B(2; 0) vào phương trình y = ax - 2, ta có:
0 = a(2) - 2
2a = 2
a = 1
Vậy, phương trình đường thẳng cần tìm là y = x - 2.
Hàm số bậc nhất được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã hiểu rõ cách giải bài 8 trang 75 Vở thực hành Toán 9. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!