Bài 9 trang 106 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 9 trang 106 VTH Toán 9 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC và O là trung điểm của cạnh AB. a) Tìm một phép quay tâm O biến điểm A thành điểm B và biến điểm B thành điểm A. b) Phép quay trên biến điểm C thành điểm D. Hãy chứng tỏ rằng ACBD là một hình bình hành.
Đề bài
Cho tam giác ABC và O là trung điểm của cạnh AB.
a) Tìm một phép quay tâm O biến điểm A thành điểm B và biến điểm B thành điểm A.
b) Phép quay trên biến điểm C thành điểm D. Hãy chứng tỏ rằng ACBD là một hình bình hành.
Phương pháp giải - Xem chi tiết
a) Phép quay ngược chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
b) Chứng minh AB và CD cắt nhau tại trung điểm O của mỗi đoạn nên ACBD là hình bình hành.
Lời giải chi tiết
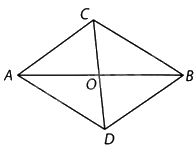
a) Phép quay ngược chiều \({180^o}\) tâm O biến A thành B và biến B thành A.
b) Nếu phép quay trên biến C thành D thì C và D; A và B đối xứng với nhau qua O.
Do đó hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn.
Do đó ACBD là hình bình hành.
Bài 9 trang 106 Vở thực hành Toán 9 tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đề bài: (Đề bài cụ thể của bài 9 sẽ được trình bày ở đây. Ví dụ: Cho hàm số y = 2x - 3. Tìm tọa độ giao điểm của đồ thị hàm số với trục Ox và trục Oy.)
Lời giải:
Ngoài bài tập tìm giao điểm, bài 9 trang 106 VTH Toán 9 tập 2 và các bài tập tương tự thường gặp các dạng sau:
Ví dụ 1: (Đề bài ví dụ về xác định hệ số a và b)
Lời giải: (Lời giải chi tiết cho ví dụ 1)
Ví dụ 2: (Đề bài ví dụ về kiểm tra điểm thuộc đồ thị)
Lời giải: (Lời giải chi tiết cho ví dụ 2)
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em học sinh có thể luyện tập thêm các bài tập sau:
Bài 9 trang 106 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất và ứng dụng của nó. Bằng cách nắm vững lý thuyết, phương pháp giải và luyện tập thường xuyên, các em học sinh sẽ tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.