Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 83, 84 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn thì sẽ là người thắng cuộc. Nếu hai số được chọn bằng nhau thì kết quả là hòa. Tính xác suất của các biến cố sau: a) A: “Bạn Minh thắng”; b) B: “Bạn Huy thắng”.
Đề bài
Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn thì sẽ là người thắng cuộc. Nếu hai số được chọn bằng nhau thì kết quả là hòa. Tính xác suất của các biến cố sau:
a) A: “Bạn Minh thắng”;
b) B: “Bạn Huy thắng”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
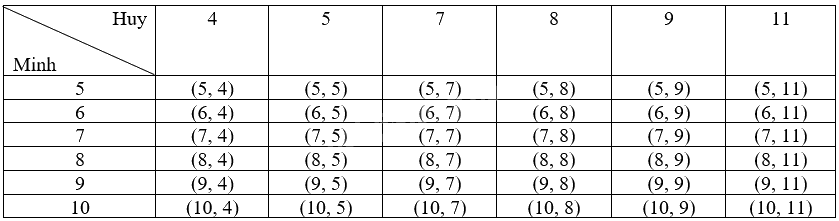
Mỗi ô ở bảng trên là một kết quả có thể. Có 36 kết quả có thể là đồng khả năng.
a) Có 17 kết quả thuận lợi cho biến cố A là các ô (a, b) ở đó \(a > b\). Vậy \(P\left( A \right) = \frac{{17}}{{36}}\).
b) Có 15 kết quả thuận lợi cho biến cố B là các ô (a, b) ở đó \(a < b\). Vậy \(P\left( B \right) = \frac{{15}}{{36}} = \frac{5}{{12}}\).
Bài 3 trang 83, 84 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 3 thường bao gồm các dạng bài tập sau:
Đề bài: Các hàm số sau có phải là hàm số bậc nhất không? Nếu có, hãy xác định hệ số a.
Giải:
Đề bài: Cho hàm số y = (m - 2)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất.
Giải:
Để hàm số y = (m - 2)x + 3 là hàm số bậc nhất thì m - 2 ≠ 0, tức là m ≠ 2.
Đề bài: Vẽ đồ thị của hàm số y = 2x - 1.
Giải:
Để vẽ đồ thị của hàm số y = 2x - 1, ta cần xác định hai điểm thuộc đồ thị. Ví dụ:
Nối hai điểm A và B, ta được đồ thị của hàm số y = 2x - 1.
Việc giải bài 3 trang 83, 84 Vở thực hành Toán 9 tập 2 một cách thành thạo sẽ giúp các em củng cố kiến thức về hàm số bậc nhất và chuẩn bị tốt cho các bài học tiếp theo. Chúc các em học tập tốt!