Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Bài viết này tập trung vào việc giải các câu hỏi trắc nghiệm trang 116 Vở thực hành Toán 9, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, dễ hiểu, kèm theo các giải thích rõ ràng để giúp các em hiểu rõ bản chất của từng bài toán.
Cho hai đường tròn (O; R) và (O’; r) với (R > r) cắt nhau tại hai điểm phân biệt và (OO' = d). Khẳng định nào sau đây là đúng? A. (d = R - r). B. (d > R + r). C. (R - r < d < R + r). D. (d < R - r).
Trả lời Câu 2 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; 5cm) và (O’; 3cm) với \(OO' = 12cm\). Khẳng định nào sau đây đúng về vị trí tương đối của hai đường tròn?
A. Hai đường tròn cắt nhau.
B. Hai đường tròn tiếp xúc ngoài.
C. Hai đường tròn ở ngoài nhau.
D. Hai đường tròn tiếp xúc trong.
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) ở ngoài nhau khi \(OO' > R + r\).
Lời giải chi tiết:
Vì \(5 + 3 = 8 < 12 = OO'\) nên hai đường tròn ở ngoài nhau.
Chọn C
Trả lời Câu 1 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; R) và (O’; r) với \(R > r\) cắt nhau tại hai điểm phân biệt và \(OO' = d\). Khẳng định nào sau đây là đúng?
A. \(d = R - r\).
B. \(d > R + r\).
C. \(R - r < d < R + r\).
D. \(d < R - r\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r < d < R + r\).
Lời giải chi tiết:
Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r < d < R + r\).
Chọn C
Trả lời Câu 3 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau biết \(OO' = 10cm\). Khi đó:
A. \(R = 4cm\).
B. \(R = 14cm\).
C. \(R = 10cm\).
D. \(R = 6cm\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài khi \(OO' = R + r\).
Lời giải chi tiết:
Vì hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau nên \(OO' = 4 + R\), suy ra \(10 = 4 + R\) nên \(R = 6cm\)
Chọn D
Trả lời Câu 4 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B trong đó OA là tiếp tuyến của (O’). Biết rằng \(OA = 20cm\) và \(O'A = 15cm\). Độ dài dây AB là:
A. 24cm.
B. 12cm.
C. 25cm.
D. 22cm.
Phương pháp giải:
+ Chứng minh tam giác O’AO vuông tại A. Theo định lí Pythagore tính được OO.
+ Chứng minh OO’ là đường trung trực của AB.
+ Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO'\).
+ Ta có: \(AI.OO' = O'A.AO\left( { = 2.{S_{\Delta O'AO}}} \right)\), từ đó tính được AI, do đó tính được AB.
Lời giải chi tiết:
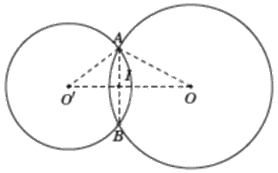
Vì OA là tiếp tuyến của (O’) nên \(O'A \bot OA\). Do đó, tam giác OAO’ vuông tại A. Theo định lí Pythagore ta có: \(OO{'^2} = O{A^2} + O'{A^2} = {20^2} + {15^2} = 625\) nên \(OO' = 25cm\).
Ta có \(OA = OB\) (bán kính (O)) nên O thuộc đường trung trực của AB, \(O'A = O'B\) (bán kính (O’)) nên O’ thuộc đường trung trực của AB. Do đó, OO’ là đường trung trực của AB.
Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO'\).
Ta có: \(AI.OO' = O'A.AO\left( { = 2.{S_{\Delta O'AO}}} \right)\) nên \(AI = \frac{{O'A.OA}}{{OO'}} = \frac{{15.20}}{{25}} = 12\left( {cm} \right)\). Do đó, \(AB = 2AI = 24cm\)
Chọn A
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; R) và (O’; r) với \(R > r\) cắt nhau tại hai điểm phân biệt và \(OO' = d\). Khẳng định nào sau đây là đúng?
A. \(d = R - r\).
B. \(d > R + r\).
C. \(R - r < d < R + r\).
D. \(d < R - r\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r < d < R + r\).
Lời giải chi tiết:
Hai đường tròn (O; R) và (O’; r) cắt nhau khi \(R - r < d < R + r\).
Chọn C
Trả lời Câu 2 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; 5cm) và (O’; 3cm) với \(OO' = 12cm\). Khẳng định nào sau đây đúng về vị trí tương đối của hai đường tròn?
A. Hai đường tròn cắt nhau.
B. Hai đường tròn tiếp xúc ngoài.
C. Hai đường tròn ở ngoài nhau.
D. Hai đường tròn tiếp xúc trong.
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) ở ngoài nhau khi \(OO' > R + r\).
Lời giải chi tiết:
Vì \(5 + 3 = 8 < 12 = OO'\) nên hai đường tròn ở ngoài nhau.
Chọn C
Trả lời Câu 3 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau biết \(OO' = 10cm\). Khi đó:
A. \(R = 4cm\).
B. \(R = 14cm\).
C. \(R = 10cm\).
D. \(R = 6cm\).
Phương pháp giải:
Hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài khi \(OO' = R + r\).
Lời giải chi tiết:
Vì hai đường tròn (O; 4cm) và (O’; R cm) tiếp xúc ngoài nhau nên \(OO' = 4 + R\), suy ra \(10 = 4 + R\) nên \(R = 6cm\)
Chọn D
Trả lời Câu 4 trang 116 Vở thực hành Toán 9
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B trong đó OA là tiếp tuyến của (O’). Biết rằng \(OA = 20cm\) và \(O'A = 15cm\). Độ dài dây AB là:
A. 24cm.
B. 12cm.
C. 25cm.
D. 22cm.
Phương pháp giải:
+ Chứng minh tam giác O’AO vuông tại A. Theo định lí Pythagore tính được OO.
+ Chứng minh OO’ là đường trung trực của AB.
+ Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO'\).
+ Ta có: \(AI.OO' = O'A.AO\left( { = 2.{S_{\Delta O'AO}}} \right)\), từ đó tính được AI, do đó tính được AB.
Lời giải chi tiết:
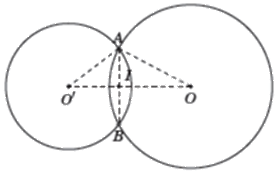
Vì OA là tiếp tuyến của (O’) nên \(O'A \bot OA\). Do đó, tam giác OAO’ vuông tại A. Theo định lí Pythagore ta có: \(OO{'^2} = O{A^2} + O'{A^2} = {20^2} + {15^2} = 625\) nên \(OO' = 25cm\).
Ta có \(OA = OB\) (bán kính (O)) nên O thuộc đường trung trực của AB, \(O'A = O'B\) (bán kính (O’)) nên O’ thuộc đường trung trực của AB. Do đó, OO’ là đường trung trực của AB.
Gọi I là giao điểm của OO’ và AB. Khi đó, \(AI = \frac{1}{2}AB\) và \(AI \bot OO'\).
Ta có: \(AI.OO' = O'A.AO\left( { = 2.{S_{\Delta O'AO}}} \right)\) nên \(AI = \frac{{O'A.OA}}{{OO'}} = \frac{{15.20}}{{25}} = 12\left( {cm} \right)\). Do đó, \(AB = 2AI = 24cm\)
Chọn A
Trang 116 Vở thực hành Toán 9 thường chứa các câu hỏi trắc nghiệm liên quan đến các chủ đề như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, phương trình bậc hai một ẩn, và các ứng dụng thực tế của đại số. Dưới đây là giải chi tiết từng câu hỏi:
Cho hàm số y = 2x + 3. Giá trị của y khi x = -1 là:
Giải: Thay x = -1 vào hàm số y = 2x + 3, ta được: y = 2*(-1) + 3 = -2 + 3 = 1. Vậy đáp án đúng là A.
Nghiệm của hệ phương trình sau là:
x + y = 5
x - y = 1
Giải: Cộng hai phương trình, ta được: 2x = 6 => x = 3. Thay x = 3 vào phương trình x + y = 5, ta được: 3 + y = 5 => y = 2. Vậy nghiệm của hệ phương trình là (3, 2), đáp án đúng là A.
Phương trình bậc hai x2 - 5x + 6 = 0 có nghiệm là:
Giải: Ta có a = 1, b = -5, c = 6. Tính delta: Δ = b2 - 4ac = (-5)2 - 4*1*6 = 25 - 24 = 1. Vì Δ > 0, phương trình có hai nghiệm phân biệt: x1 = (-b + √Δ) / 2a = (5 + 1) / 2 = 3 và x2 = (-b - √Δ) / 2a = (5 - 1) / 2 = 2. Vậy đáp án đúng là A.
Để giải nhanh các câu hỏi trắc nghiệm Toán 9, bạn nên:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập, và các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| x1 + x2 = -b/a | Tổng hai nghiệm của phương trình bậc hai |
| x1 * x2 = c/a | Tích hai nghiệm của phương trình bậc hai |
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 116 Vở thực hành Toán 9. Chúc các em học tập tốt!