Bài 5 trang 66 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường liên quan đến các kiến thức về hàm số bậc nhất và ứng dụng của chúng.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
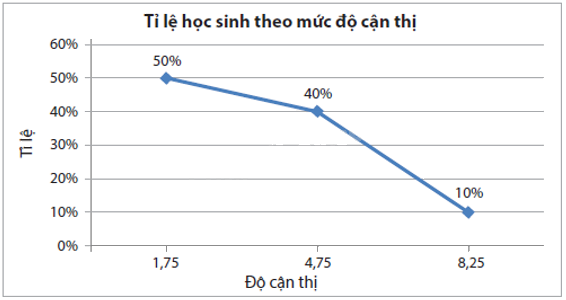
Qua đợt khám mắt, lớp 9A có 20 học sinh bị cận thị trong đó có 10 học sinh bị cận thị nhẹ, 8 học sinh cận thị vừa và 2 học sinh cận thị nặng. Biết rằng cận thị có số đo từ 0,25 đến dưới 3,25 dioptre là cận thị nhẹ, từ 3,25 đến dưới 6,25 dioptre là cận thị vừa; từ 6,25 đến dưới 10,25 dioptre là cận thị nặng. a) Lập bảng tần số và bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này. b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm thu
Đề bài
Qua đợt khám mắt, lớp 9A có 20 học sinh bị cận thị trong đó có 10 học sinh bị cận thị nhẹ, 8 học sinh cận thị vừa và 2 học sinh cận thị nặng. Biết rằng cận thị có số đo từ 0,25 đến dưới 3,25 dioptre là cận thị nhẹ, từ 3,25 đến dưới 6,25 dioptre là cận thị vừa; từ 6,25 đến dưới 10,25 dioptre là cận thị nặng.
a) Lập bảng tần số và bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm thu được ở câu a.
Phương pháp giải - Xem chi tiết
a) Bảng tần số ghép nhóm:
+ Tìm tần số của từng nhóm: Tần số \({m_i}\) của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) là số giá trị của mẫu số liệu lớn hơn hoặc bằng \({a_i}\) và nhỏ hơn \({a_{i + 1}}\).
+ Lập bảng tần số ghép nhóm:

Bảng tần số tương đối ghép nhóm:
+ Tính tần số tương đối ứng với các giá trị trong mẫu dữ liệu: Nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) có tần số \({m_i}\) thì có tần số tương đối là: \({f_i} = \frac{{{m_i}}}{n}.100\left( \% \right)\) với m là tổng tất cả các tần số có trong mẫu số liệu.
+ Lập bảng tần số tương đối ghép nhóm:

b) Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho các nhóm số liệu \(\left[ {{a_i};{a_{i + 1}}} \right)\) với \(i = 1,2,3,..,k\).
Bước 2: Vẽ trục ngang để biểu diễn các giá trị đại diện cho nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối.
Bước 3: Với mỗi giá trị đại diện \({x_i}\) trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
Lời giải chi tiết
a) Bảng tần số ghép nhóm:

Tổng số học sinh bị cận thị là 20. Tỉ lệ học sinh bị cận thị ở các mức nhẹ, nhẹ vừa, nặng tương ứng là: \(\frac{{10}}{{20}}.100\% = 50\% ;\frac{8}{{20}}.100\% = 40\% ;\frac{2}{{20}}.100\% = 10\% \).
Ta có bảng tần số tương đối như sau:

b) Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bài 5 trang 66 Vở thực hành Toán 9 tập 2 thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định hàm số, tìm các điểm thuộc đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số.
Bài tập 5 thường bao gồm các dạng bài sau:
Để giải bài 5 trang 66 Vở thực hành Toán 9 tập 2 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho một số dạng bài tập thường gặp trong bài 5 trang 66 Vở thực hành Toán 9 tập 2:
Cho đồ thị hàm số đi qua hai điểm A(0; 2) và B(1; 5). Hãy xác định hàm số bậc nhất y = ax + b.
Lời giải:
Vì đồ thị hàm số đi qua điểm A(0; 2), ta có: 2 = a * 0 + b => b = 2.
Vì đồ thị hàm số đi qua điểm B(1; 5), ta có: 5 = a * 1 + b => 5 = a + 2 => a = 3.
Vậy hàm số bậc nhất cần tìm là y = 3x + 2.
Cho hàm số y = -2x + 1. Hãy tìm giá trị của y khi x = -1.
Lời giải:
Thay x = -1 vào hàm số y = -2x + 1, ta có: y = -2 * (-1) + 1 = 2 + 1 = 3.
Vậy khi x = -1, thì y = 3.
Để học tốt Toán 9, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với hướng dẫn chi tiết và lời giải trên, các em học sinh sẽ tự tin giải bài 5 trang 66 Vở thực hành Toán 9 tập 2 một cách hiệu quả. Chúc các em học tốt!