Giải bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2

Giải bài 3 trang 75, 76 vở thực hành Toán 9 tập 2

Giải bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2

Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.

Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.

Có hai tấm bìa cứng hình tròn A và B. Tấm bìa cứng A được chia làm 4 hình quạt như nhau, ghi các số 5, 6, 7, 8. Tấm bìa cứng B được chia làm 5 hình quạt như nhau, ghi các số 1, 2, 3, 4, 5. Mỗi tấm bìa được gắn vào trục quay có mũi tên cố định ở tâm. Bạn An quay tấm bìa A và bạn Bình quay tấm bìa B. Giả sử khi tấm bìa A và B dừng lại, mũi tên chỉ tương ứng vào hình quạt ghi số a và ghi số b. Tính xác suất các biến cố sau: • E: “Trong hai số a và b có ít nhất một số 5”; • F: “Tích ab là số lẻ”.

Đề bài

E: “Trong hai số a và b có ít nhất một số 5”;
F: “Tích ab là số lẻ”.

Phương pháp giải - Xem chi tiết Giải bài 3 trang 75, 76 vở thực hành Toán 9 tập 2 1

Cách tính xác suất của một biến cố E:

Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).

Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.

Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.

Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).

Lời giải chi tiết

Ta lập bảng sau:

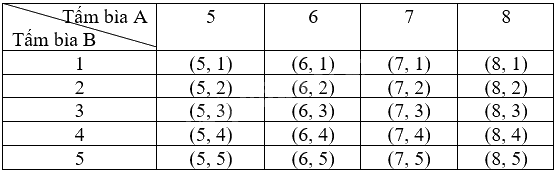
Giải bài 3 trang 75, 76 vở thực hành Toán 9 tập 2 2

Mỗi ô trong bảng là một kết quả có thể. Có 20 kết quả có thể là đồng khả năng.

Không gian mẫu là

\(\Omega = {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (7, 1), (7, 2), (7, 3), (7, 4), (7, 5), (8, 1), (8, 2), (8, 3), (8, 4), (8, 5)}.\)

Các kết quả thuận lợi cho biến cố E là (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (6, 5), (7, 5), (8, 5).

Vậy \(P\left( E \right) = \frac{8}{{20}} = \frac{2}{5}\).

Các kết quả thuận lợi cho biến cố F là (5, 1), (5, 3), (5, 5), (7, 1), (7, 3), (7, 5).

Vậy \(P\left( F \right) = \frac{6}{{20}} = \frac{3}{{10}}\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 3 trang 75, 76 vở thực hành Toán 9 tập 2 đặc sắc thuộc chuyên mục toán 9 sgk trên nền tảng toán math. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2: Ôn tập chương hàm số bậc nhất

Bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.

Nội dung bài tập

Bài 3 thường bao gồm các dạng bài tập sau:

Xác định hàm số bậc nhất: Cho một công thức, học sinh cần xác định xem đó có phải là hàm số bậc nhất hay không.
Tìm hệ số a: Cho hàm số bậc nhất, học sinh cần tìm hệ số a dựa trên các thông tin đã cho.
Xác định đường thẳng: Vẽ đồ thị của hàm số bậc nhất và xác định các điểm đặc biệt trên đồ thị.
Ứng dụng hàm số bậc nhất vào giải toán: Giải các bài toán thực tế liên quan đến hàm số bậc nhất, ví dụ như tính quãng đường, thời gian, vận tốc.

Hướng dẫn giải chi tiết

Để giải bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:

Định nghĩa hàm số bậc nhất: Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Hệ số a: Hệ số a xác định độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải.
Hệ số b: Hệ số b là tung độ gốc, tức là giao điểm của đường thẳng với trục Oy.

Dưới đây là hướng dẫn giải chi tiết một số dạng bài tập thường gặp:

Dạng 1: Xác định hàm số bậc nhất

Để xác định một công thức có phải là hàm số bậc nhất hay không, học sinh cần kiểm tra xem công thức đó có dạng y = ax + b hay không, với a ≠ 0. Ví dụ, công thức y = 2x + 3 là hàm số bậc nhất, trong khi công thức y = x² + 1 không phải là hàm số bậc nhất.

Dạng 2: Tìm hệ số a

Để tìm hệ số a, học sinh có thể sử dụng các thông tin đã cho trong bài toán, ví dụ như hai điểm thuộc đồ thị của hàm số. Giả sử đồ thị của hàm số y = ax + b đi qua hai điểm A(x₁, y₁) và B(x₂, y₂), ta có thể giải hệ phương trình sau để tìm a và b:

y₁ = ax₁ + b
y₂ = ax₂ + b

Dạng 3: Xác định đường thẳng

Để vẽ đồ thị của hàm số bậc nhất, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Sau đó, nối hai điểm này lại với nhau để được đường thẳng. Học sinh cũng có thể sử dụng các thông tin về hệ số a và b để xác định các đặc điểm của đường thẳng, ví dụ như độ dốc, tung độ gốc.

Ví dụ minh họa

Bài tập: Cho hàm số y = -2x + 1. Hãy xác định hệ số a và vẽ đồ thị của hàm số.

Giải:

Hệ số a là -2. Vì a < 0, đường thẳng đi xuống từ trái sang phải.
Để vẽ đồ thị, ta xác định hai điểm thuộc đồ thị, ví dụ A(0, 1) và B(1, -1).
Nối hai điểm A và B lại với nhau để được đường thẳng.

Luyện tập thêm

Để củng cố kiến thức về hàm số bậc nhất, học sinh nên luyện tập thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 9 để được hướng dẫn chi tiết hơn.

Kết luận

Bài 3 trang 75, 76 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể giải quyết bài tập một cách hiệu quả và đạt kết quả tốt trong môn Toán.