Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 5 trang 122, 123 Vở thực hành Toán 9, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng bạn trên con đường chinh phục môn Toán.
Cho đường tròn (O) đường kính BC và điểm A (khác B và C). a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì A nằm trên (O). b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC. c) Với cùng giả thiết câu b, tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng (BC = 6cm).
Đề bài
Cho đường tròn (O) đường kính BC và điểm A (khác B và C).
a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì A nằm trên (O).
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
c) Với cùng giả thiết câu b, tính độ dài cung AC và diện tích hình quạt nằm trong (O) giới hạn bởi các bán kính OA và OC, biết rằng \(BC = 6cm\).
Phương pháp giải - Xem chi tiết
a) Gọi \(R = \frac{{BC}}{2}\) là bán kính của đường tròn.
+ Nếu \(A \in \left( {O;R} \right)\) thì \(OA = R\). Khi đó, tam giác ABC có \(OB = OC = OA\) bằng R nên là trung tuyến ứng với cạnh huyền BC (góc BAC vuông).
+ Nếu tam giác ABC vuông tại A thì \(OA = OB = OC\) bằng R, nghĩa là \(AO = \frac{{BC}}{2} = R\). Do đó, điểm A nằm trên (O).
b) + Chứng minh tam giác ABO đều O vì \(OA = OB = AB = R\). Do đó, \(\widehat {ABO} = \widehat {ABC} = {60^o}\).
+ Tính được \(\widehat {BCA} = {30^o}\).
c) Tính góc AOC từ đó suy ra số đo cung AC nhỏ.
+ Độ dài cung AC là \(l = \frac{{120}}{{180}}.\pi .3\)
+ Diện tích của nó bằng \(S = \frac{{120}}{{360}}.\pi {.3^2}\)
Lời giải chi tiết
a) Gọi \(R = \frac{{BC}}{2}\) là bán kính của đường tròn.
Nếu \(A \in \left( {O;R} \right)\) thì \(OA = R\). Khi đó, tam giác ABC có \(OB = OC = OA\) bằng R nên là trung tuyến ứng với cạnh huyền BC (góc BAC vuông).
Ngược lại, nếu tam giác ABC vuông tại A thì trung tuyến OA bằng một nửa cạnh huyền BC, nghĩa là \(AO = \frac{{BC}}{2} = R\). Do đó, điểm A nằm trên (O).
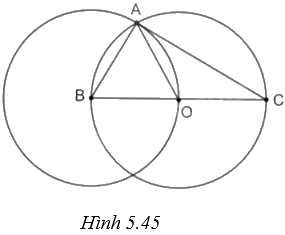
b) (H.5.45)
Vì \(BO = \frac{{BC}}{2} = R\) nên khi A là một trong hai giao điểm đường tròn (B; BO) với đường tròn (O) thì tam giác ABO đều O vì \(OA = OB = AB = R\). Do đó, \(\widehat {ABO} = \widehat {ABC} = {60^o}\).
Theo câu a, ABC là tam giác vuông tại A và có \(\widehat {ABC} = {60^o}\) nên \(\widehat {BCA} = {30^o}\).
c) Từ câu b, ta có \(\widehat {AOB} = {60^o}\), suy ra sđ$\overset\frown{AC}=\widehat{AOC}={{180}^{o}}-{{60}^{o}}={{120}^{o}}$.
Mặt khác \(R = \frac{{BC}}{2} = 3\left( {cm} \right)\) nên độ dài cung AC là \(l = \frac{{120}}{{180}}.\pi .3 = 2\pi \left( {cm} \right)\).
Hình quạt giới hạn bởi hai bán kính OA, OC ứng với cung \({120^o}\) nên diện tích của nó bằng \(S = \frac{{120}}{{360}}.\pi {.3^2} = 3\pi \left( {c{m^2}} \right)\).
Bài 5 trang 122, 123 Vở thực hành Toán 9 thường thuộc chương trình học về hàm số bậc nhất. Các bài tập trong phần này tập trung vào việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số bậc nhất vào giải quyết các bài toán thực tế.
Để giải quyết bài 5 trang 122, 123 Vở thực hành Toán 9 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Trong phần này, bạn cần xác định hệ số góc và tung độ gốc của các hàm số bậc nhất cho trước. Để làm điều này, bạn chỉ cần so sánh hàm số với dạng tổng quát y = ax + b. Ví dụ, nếu hàm số là y = 2x - 3, thì hệ số góc a = 2 và tung độ gốc b = -3.
Để viết phương trình đường thẳng, bạn cần biết ít nhất hai điểm thuộc đường thẳng đó. Sau đó, bạn có thể sử dụng công thức tính hệ số góc và tung độ gốc để tìm ra phương trình đường thẳng.
Ví dụ, nếu đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), thì hệ số góc a được tính bằng công thức: a = (y2 - y1) / (x2 - x1). Sau đó, bạn có thể sử dụng một trong hai điểm A hoặc B và hệ số góc a để tìm ra tung độ gốc b.
Trong phần này, bạn cần sử dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Ví dụ, bạn có thể sử dụng hàm số bậc nhất để tính quãng đường đi được của một vật chuyển động đều trong một khoảng thời gian nhất định.
Bài toán: Một ô tô đi từ A đến B với vận tốc 60 km/h. Hãy viết hàm số biểu thị quãng đường đi được của ô tô theo thời gian.
Giải: Gọi s là quãng đường đi được của ô tô (km) và t là thời gian ô tô đi (giờ). Ta có hàm số s = 60t.
Bài 5 trang 122, 123 Vở thực hành Toán 9 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.