Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 7 trang 124 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho điểm B nằm giữa hai điểm A và C, sao cho (AB = 2cm) và (BC = 1cm). Vẽ các đường tròn (A; 1,5cm), (B; 3cm) và (C; 2cm). Hãy xác định các cặp đường tròn: a) Cắt nhau; b) Không giao nhau; c) Tiếp xúc với nhau.
Đề bài
Cho điểm B nằm giữa hai điểm A và C, sao cho \(AB = 2cm\) và \(BC = 1cm\). Vẽ các đường tròn (A; 1,5cm), (B; 3cm) và (C; 2cm). Hãy xác định các cặp đường tròn:
a) Cắt nhau;
b) Không giao nhau;
c) Tiếp xúc với nhau.
Phương pháp giải - Xem chi tiết
Hai đường tròn (O; R) và (O’; r) (với \(R > r\)). Khi đó:
+ Hai đường tròn ở ngoài nhau khi \(OO' > R + r\).
+ Hai đường tròn tiếp xúc ngoài khi \(OO' = R + r\).
+ Hai đường tròn cắt nhau khi \(R - r < OO' < R + r\).
+ Hai đường tròn tiếp xúc trong khi \(OO' = R - r\).
+ Đường tròn (O) đựng (O’) khi \(OO' < R - r\).
Lời giải chi tiết
(H.5.47)
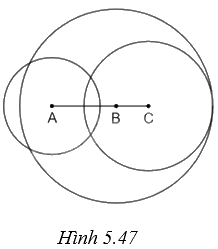
Gọi \({R_A},{R_B}\) và \({R_C}\) lần lượt là bán kính các đường tròn (A), (B), (C). Theo đề bài, ta có \({R_A} = 1,5cm,{R_B} = 3cm,{R_C} = 2cm\), \(AB = 2cm\), \(BC = 1cm\) và \(CA = 3cm\). Ta có:
+) \({R_B} - {R_A} = 1,5 < AB < {R_B} + {R_A} = 4,5\). Do đó (A) và (B) cắt nhau.
+) \({R_C} - {R_A} = 0,5 < CA < {R_C} + {R_A} = 3,5\). Do đó (A) và (C) cắt nhau.
+) \(BC = {R_B} - {R_C}\). Do đó, (B) và (C) tiếp xúc trong.
Không có cặp đường tròn nào không giao nhau.
Bài 7 trang 124 Vở thực hành Toán 9 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và tìm điều kiện để hàm số đồng biến hoặc nghịch biến. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 9.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 7 trang 124 Vở thực hành Toán 9, chúng tôi sẽ cung cấp lời giải chi tiết cho từng dạng bài tập:
Cho hàm số y = (m - 2)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất.
Lời giải:
Để hàm số y = (m - 2)x + 3 là hàm số bậc nhất, thì hệ số a phải khác 0. Do đó, ta có:
m - 2 ≠ 0
m ≠ 2
Vậy, với m ≠ 2, hàm số y = (m - 2)x + 3 là hàm số bậc nhất.
Cho hàm số y = 2x - 1. Tính giá trị của y khi x = 3.
Lời giải:
Thay x = 3 vào hàm số y = 2x - 1, ta được:
y = 2 * 3 - 1 = 6 - 1 = 5
Vậy, khi x = 3, thì y = 5.
Cho hàm số y = (k + 1)x + 2. Tìm giá trị của k để hàm số đồng biến.
Lời giải:
Để hàm số y = (k + 1)x + 2 đồng biến, thì hệ số a phải lớn hơn 0. Do đó, ta có:
k + 1 > 0
k > -1
Vậy, với k > -1, hàm số y = (k + 1)x + 2 đồng biến.
Bài 7 trang 124 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.
Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác tại giaitoan.edu.vn!