Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 106 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các phương pháp giải bài tập hiệu quả.
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình sau đây. Biết (widehat {BEC} = {40^o}) và (widehat {DFC} = {20^o}), tính số đo các góc của tứ giác ABCD.
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình sau đây. Biết \(\widehat {BEC} = {40^o}\) và \(\widehat {DFC} = {20^o}\), tính số đo các góc của tứ giác ABCD.
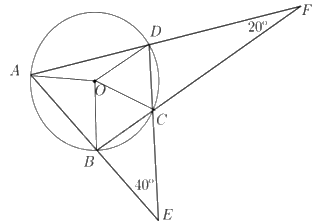
Phương pháp giải - Xem chi tiết
+ Tính được \(\hat A + \hat D = {180^ \circ } - \widehat E = {140^ \circ }\), suy ra \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {AOB} + \widehat {BOC}} \right) = {140^o}\), hay \(\frac{1}{2}\left( {{{360}^o} + \widehat {BOC} - \widehat {AOD}} \right) = {140^o}\) nên \(\widehat {DOA} - \widehat {BOC} = {80^o}\) (1)
+ Tương tự tính được \(\widehat {AOB} - \widehat {COD} = {40^o}\) (2)
+ Cộng vế với vế của (1) và (2) ta có: \(\widehat {AOB} + \widehat {DOA} - \widehat {COD} - \widehat {BOC} = {120^o}\) hay , biết \(sđ\overset\frown{DAB}+sđ\overset\frown{BCD}={{360}^{o}}\)
+ $\widehat{C}=\frac{1}{2}sđ\overset\frown{DAB};\widehat{A}=\frac{1}{2}sđ\overset\frown{BCD}$ nên tính được góc C và A.
+ Trừ vế với vế của (1) cho (2), ta có \(\widehat {DOA} + \widehat {COD} - \widehat {AOB} - \widehat {BOC} = {40^o}\) hay \(sđ\overset\frown{CDA}-sđ\overset\frown{ABC}={{40}^{o}}\), biết \(sđ\overset\frown{CDA}+sđ\overset\frown{ABC}={{360}^{o}}\).
+ $\widehat{B}=\frac{1}{2}sđ\overset\frown{CDA};\widehat{D}=\frac{1}{2}sđ\overset\frown{ABC}$ nên tính được góc B và góc D.
Lời giải chi tiết
Vì tổng các góc trong tam giác \(ADE\) bằng 180o nên \(\hat A + \hat D = {180^ \circ } - \widehat E = {140^ \circ }\).
Do vậy \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {AOB} + \widehat {BOC}} \right) = {140^o}\)
Suy ra \(\frac{1}{2}\left( {{{360}^o} + \widehat {BOC} - \widehat {AOD}} \right) = {140^o}\), hay \(\widehat {DOA} - \widehat {BOC} = {80^o}\) (1)
Mặt khác, tổng các góc trong tam giác ABF bằng 180o nên \(\hat A + \hat B = {180^ \circ } - \widehat F = {160^ \circ }\).
Do vậy \(\frac{1}{2}\left( {\widehat {BOC} + \widehat {COD}} \right) + \frac{1}{2}\left( {\widehat {COD} + \widehat {DOA}} \right) = {160^o}\)
Suy ra \(\frac{1}{2}\left( {{{360}^o} + \widehat {COD} - \widehat {AOB}} \right) = {160^o}\), hay \(\widehat {AOB} - \widehat {COD} = {40^o}\) (2)
Cộng vế với vế của (1) và (2), ta được \(\widehat {AOB} + \widehat {DOA} - \widehat {COD} - \widehat {BOC} = {120^o}\)
hay \(sđ\overset\frown{DAB}-sđ\overset\frown{BCD}={{120}^{o}}\), chú ý rằng \(sđ\overset\frown{DAB}+sđ\overset\frown{BCD}={{360}^{o}}\)
Suy ra: $\widehat{C}=\frac{1}{2}sđ\overset\frown{DAB}=\frac{{{120}^{o}}+{{360}^{o}}}{4}={{120}^{o}}$; $\widehat{A}=\frac{1}{2}sđ\overset\frown{BCD}=\frac{{{360}^{o}}-{{120}^{o}}}{4}={{60}^{o}}$.
Trừ vế với vế của (1) cho (2), ta được \(\widehat {DOA} + \widehat {COD} - \widehat {AOB} - \widehat {BOC} = {40^o}\)
hay \(sđ\overset\frown{CDA}-sđ\overset\frown{ABC}={{40}^{o}}\), chú ý rằng \(sđ\overset\frown{CDA}+sđ\overset\frown{ABC}={{360}^{o}}\)
Suy ra: $\widehat{B}=\frac{1}{2}sđ\overset\frown{CDA}=\frac{{{40}^{o}}+{{360}^{o}}}{4}={{100}^{o}}$; $\widehat{D}=\frac{1}{2}sđ\overset\frown{ABC}=\frac{{{360}^{o}}-{{40}^{o}}}{4}={{80}^{o}}$.
Bài 2 trang 106 Vở thực hành Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là cách xác định hệ số góc và phương trình đường thẳng.
Trước khi bắt đầu giải bài, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tránh được những sai sót không đáng có và tập trung vào việc tìm ra lời giải chính xác.
Dưới đây là lời giải chi tiết cho bài 2 trang 106 Vở thực hành Toán 9 tập 2. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng, dễ hiểu để giúp các em nắm vững phương pháp giải bài.
Ngoài bài toán tìm tọa độ giao điểm, bài 2 trang 106 Vở thực hành Toán 9 tập 2 còn có thể xuất hiện các dạng bài tập khác như:
Để giải bài tập Toán 9 hiệu quả, học sinh nên:
Để củng cố kiến thức và kỹ năng giải bài, học sinh có thể tự giải các bài tập tương tự sau:
Bài 2 trang 106 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các phương pháp giải bài hiệu quả mà chúng tôi đã cung cấp, các em sẽ tự tin hơn trong việc học tập môn Toán.