Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 129, 130 Vở thực hành Toán 9 tập 2. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 9.
Chúng tôi sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, cùng với đáp án chính xác, giúp các em nắm vững kiến thức và tự tin hơn trong các kỳ thi.
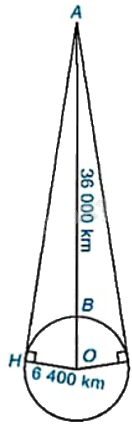
Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng (AB = 36;000km), tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị).
Đề bài
Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng \(AB = 36\;000km\), tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị).
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pythagore vào tam giác AHO vuông tại H để tính AH, từ đó đưa ra kết luận.
Lời giải chi tiết
Giả sử vị trí xa nhất trên bề mặt Trái Đất nhận được tín hiệu từ vệ tinh là điểm H. Khi đó AH là tiếp tuyến của bề mặt Trái Đất.
Khoảng cách giữa vệ tinh và tâm Trái Đất là \(AO = AB + BO = 36\;000 + 6\;400 = 42\;400\left( {km} \right)\).
Vì AH là tiếp tuyến của bề mặt Trái Đất nên \(\Delta AOH\) vuông tại H.
Áp dụng định lí Pythagore cho tam giác AHO vuông tại H, ta có:
\(A{O^2} = A{H^2} + H{O^2}\)
\(A{H^2} = A{O^2} - H{O^2} = 42\;{400^2} - 6\;{400^2} = 1\;756\;800\;000\)
\(AH = \sqrt {1\;756\;800\;000} \approx 41\;914\left( {km} \right)\).
Vậy vị trí xa nhất trên Trái Đất có thể nhận tín hiệu của vệ tinh cách vệ tinh khoảng 41 914km.
Bài 2 trang 129, 130 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 2 thường bao gồm các dạng bài tập sau:
Bài 2a yêu cầu học sinh xác định hàm số bậc nhất. Để giải bài này, học sinh cần nhớ định nghĩa về hàm số bậc nhất: y = ax + b, trong đó a và b là các số thực và a ≠ 0. Học sinh cần kiểm tra xem biểu thức đã cho có dạng y = ax + b hay không. Nếu có, thì đó là hàm số bậc nhất. Nếu không, thì đó không phải là hàm số bậc nhất.
Ví dụ: Cho hàm số y = 2x - 3. Đây là hàm số bậc nhất vì nó có dạng y = ax + b, với a = 2 và b = -3.
Bài 2b yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để giải bài này, học sinh cần giải hệ phương trình tương ứng với hai đường thẳng đó. Ví dụ: Cho hai đường thẳng y = x + 1 và y = -x + 3. Để tìm giao điểm của hai đường thẳng này, ta giải hệ phương trình:
{ y = x + 1 y = -x + 3 }
Thay y = x + 1 vào phương trình y = -x + 3, ta được: x + 1 = -x + 3. Giải phương trình này, ta được x = 1. Thay x = 1 vào phương trình y = x + 1, ta được y = 2. Vậy giao điểm của hai đường thẳng là (1; 2).
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong sách giáo khoa và sách bài tập Toán 9. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học Toán uy tín.
Bài 2 trang 129, 130 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp các em ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong các kỳ thi.