Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 3 trang 122, 123 Vở thực hành Toán 9 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
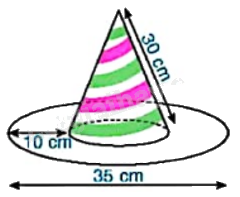
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của (c{m^2})).
Đề bài
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của \(c{m^2}\)).
Phương pháp giải - Xem chi tiết
+ Bán kính đường tròn đáy của hình nón là: \(R = \left( {35 - 2.10} \right):2 = 7,5\left( {cm} \right)\).
+ Tính diện tích xung quanh hình nón có bán kính \(35:2\left( {cm} \right)\) và đường sinh 30cm.
+ Diện tích vành mũ bằng hiệu diện tích hình tròn bán kính \(35:2cm\) và diện tích hình tròn bán kính \(\)\(\left( {35:2 - 10} \right)cm\).
+ Diện tích vải cần dùng bằng tổng diện tích xung quanh của hình nón và diện tích vành mũ.
Lời giải chi tiết
Bán kính đường tròn đáy của hình nón là \(\left( {35 - 2.10} \right):2 = 7,5\left( {cm} \right)\).
Diện tích xung quanh của hình nón là:
\({S_1} = \pi Rl = \pi .7,5.30 = 225\pi \left( {c{m^2}} \right)\).
Diện tích vành mũ (hình vành khăn) là:
\({S_2} = \pi .{\left( {35:2} \right)^2} - \pi .{\left( {15:2} \right)^2} = 250\pi \left( {c{m^2}} \right).\)
Diện tích vải cần để làm chiếc mũ là:
\(S = {S_1} + {S_2} = 225\pi + 250\pi = 475\pi \approx 1492,3\left( {c{m^2}} \right).\)
Bài 3 trang 122, 123 Vở thực hành Toán 9 tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hệ số góc, đường thẳng song song, và ứng dụng của hàm số bậc nhất vào giải quyết các bài toán thực tế.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải bài 3 trang 122, 123 Vở thực hành Toán 9 tập 2 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Bài tập: Cho hàm số y = 2x - 1. Hãy xác định hệ số góc của hàm số.
Giải: Hệ số góc của hàm số y = 2x - 1 là a = 2.
Bài tập: Cho hai đường thẳng y = 3x + 2 và y = 3x - 1. Chứng minh rằng hai đường thẳng này song song.
Giải: Ta có a1 = 3 và a2 = 3, suy ra a1 = a2. Đồng thời, b1 = 2 và b2 = -1, suy ra b1 ≠ b2. Vậy hai đường thẳng y = 3x + 2 và y = 3x - 1 song song.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn nên thực hành thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học Toán 9 để được hướng dẫn chi tiết hơn.
Khi giải bài tập về hàm số bậc nhất, bạn cần chú ý những điều sau:
Ngoài việc giải bài tập trong Vở thực hành, bạn có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, chẳng hạn như trong lĩnh vực kinh tế, vật lý, và kỹ thuật. Việc mở rộng kiến thức sẽ giúp bạn hiểu sâu hơn về môn Toán và có thể áp dụng nó vào giải quyết các vấn đề thực tế.