Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 73 Vở thực hành Toán 9. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết: a) (AB = 8cm,BC = 17cm); b) (AC = 0,9cm,AB = 1,2cm).
Đề bài
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, côsin, tang, côtang của các góc nhọn B và C khi biết:
a) \(AB = 8cm,BC = 17cm\);
b) \(AC = 0,9cm,AB = 1,2cm\).
Phương pháp giải - Xem chi tiết
- Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có
+ Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối gọi là cot của \(\alpha \).
- Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết
a) (H.4.5a)
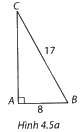
Theo định lí Pythagore, ta có \(A{C^2} + A{B^2} = B{C^2}\)
\(A{C^2} = B{C^2} - A{B^2}\)
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{17}^2} - {8^2}} = 15\left( {cm} \right)\)
Từ đó
\(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}};\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{8}{{17}};\\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{15}}{8};\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\)
b) (H.4.5b)
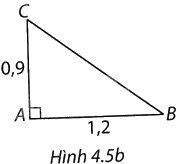
Theo Pythagore, ta có \(BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{{1,2}^2} + {{0,9}^2}} = 1,5\)
Từ đó
\(\sin B = \cos C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5},\\\cos B = \sin C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}, \\\tan B = \cot C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4},\\\cot B = \tan C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}.\)
Bài 1 trang 73 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập yêu cầu học sinh vận dụng các kiến thức đã học để xác định hệ số góc, đường thẳng song song, và giải các bài toán liên quan đến hàm số.
Bài 1 trang 73 Vở thực hành Toán 9 bao gồm các câu hỏi và bài tập sau:
Để xác định hệ số góc của đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Nếu phương trình đường thẳng được cho dưới dạng tổng quát Ax + By + C = 0, ta có thể chuyển về dạng y = ax + b để xác định a. Ví dụ, nếu phương trình là 2x + 3y - 6 = 0, ta chuyển về y = (-2/3)x + 2, suy ra hệ số góc là -2/3.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song với nhau khi và chỉ khi hệ số góc của chúng bằng nhau và hai đường thẳng không trùng nhau, tức là a1 = a2 và b1 ≠ b2.
Để xác định phương trình đường thẳng đi qua hai điểm M(x1; y1) và N(x2; y2), ta thực hiện các bước sau:
Khi giải bài toán thực tế liên quan đến hàm số bậc nhất, ta cần:
Ví dụ: Cho đường thẳng y = 2x - 1. Hãy xác định hệ số góc của đường thẳng này.
Giải: Đường thẳng y = 2x - 1 có dạng y = ax + b, với a = 2 và b = -1. Vậy hệ số góc của đường thẳng là 2.
Bài 1 trang 73 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.