Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 7 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số, tập trung vào việc giải các bài toán liên quan đến hàm số bậc nhất.
Giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết từng bước, giúp các em nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Vẽ đồ thị của các hàm số sau: a) (y = 3{x^2}); b) (y = - frac{1}{3}{x^2}).
Đề bài
Vẽ đồ thị của các hàm số sau:
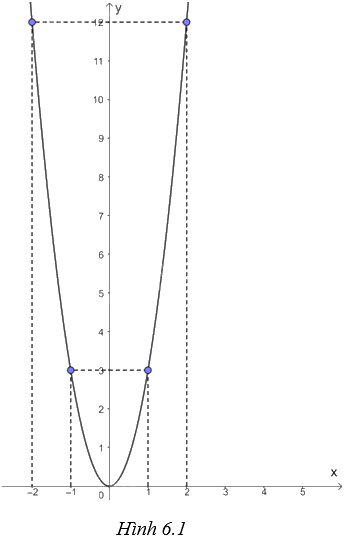
a) \(y = 3{x^2}\);
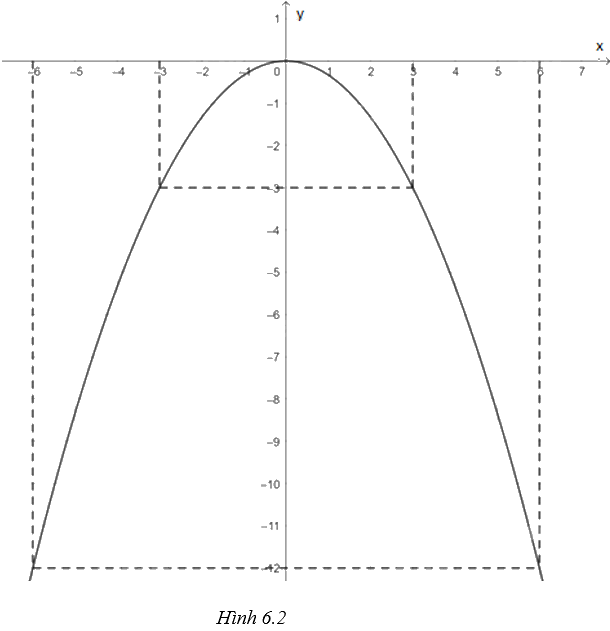
b) \(y = - \frac{1}{3}{x^2}\).
Phương pháp giải - Xem chi tiết
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải chi tiết
a) Lập bảng một số giá trị tương ứng giữa x và y:

Từ đó vẽ được đồ thị hàm số \(y = 3{x^2}\) như Hình 6.1.
b) Lập bảng một số giá trị tương ứng giữa x và y:

Từ đó vẽ được đồ thị của hàm số \(y = - \frac{1}{3}{x^2}\) như Hình 6.2.
Bài 4 trang 7 Vở thực hành Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Cụ thể, bài toán thường liên quan đến việc xác định hàm số, tìm điểm thuộc đồ thị hàm số, hoặc giải các bài toán ứng dụng liên quan đến hàm số.
Để giải quyết bài 4 trang 7 Vở thực hành Toán 9 tập 2 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho bài 4 trang 7 Vở thực hành Toán 9 tập 2. (Lưu ý: Nội dung lời giải cụ thể sẽ phụ thuộc vào từng dạng bài tập trong Vở thực hành. Ví dụ sau chỉ mang tính minh họa)
Bài toán: Cho hàm số y = 2x - 1. Tìm tọa độ điểm A thuộc đồ thị hàm số sao cho x = 3.
Lời giải:
Bài 4 trang 7 Vở thực hành Toán 9 tập 2 thường xuất hiện các dạng bài tập sau:
Để giải các bài tập trong bài 4 trang 7 Vở thực hành Toán 9 tập 2 một cách hiệu quả, các em nên:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 4 trang 7 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!