Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 2 trang 102 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho đường tròn (O; 5cm) và AB là một dây bất kì của đường tròn đó. Biết (AB = 6cm). a) Tính khoảng cách từ O đến đường thẳng AB. b) Tính (tan alpha ) nếu góc ở tâm chắn cung AB bằng (2alpha ).
Đề bài
Cho đường tròn (O; 5cm) và AB là một dây bất kì của đường tròn đó. Biết \(AB = 6cm\).
a) Tính khoảng cách từ O đến đường thẳng AB.
b) Tính \(\tan \alpha \) nếu góc ở tâm chắn cung AB bằng \(2\alpha \).
Phương pháp giải - Xem chi tiết
a) + Gọi C là trung điểm của AB. Chứng minh CO là đường cao của tam giác OAB nên OC là khoảng cách từ O đến AB.
+ Áp dụng định lí Pythagore vào tam giác AOC vuông tại C tính được OC.
b) + Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác, suy ra \(\widehat {AOC} = \alpha \).
+ Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{CA}}{{CO}}\).
Lời giải chi tiết
(H.5.10)
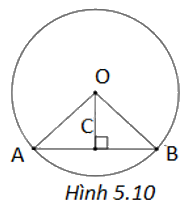
Theo giả thiết, ta có \(OA = OB = 5cm\); \(AB = 6cm\).
a) Gọi C là trung điểm của AB, ta có \(AC = CB = 3cm\). Trong tam giác AOB cân tại O \(\left( {OA = OB} \right)\) có OC là đường trung tuyến nên cũng là đường cao nghĩa là \(CO \bot AB\) tại C.
Vậy OC là khoảng cách từ O đến AB.
Trong tam giác vuông AOC, ta có: \(O{C^2} = O{A^2} - C{A^2} = {5^2} - {3^2} = 16\), suy ra \(OC = 4cm\).
Vậy khoảng cách từ O đến đường thẳng AB bằng 4cm.
b) Trong tam giác cân OAB, đường trung tuyến OC cũng là đường phân giác. Mà \(\widehat {AOB} = 2\alpha \) nên \(\widehat {AOC} = \alpha \).
Xét tam giác AOC vuông tại C, ta có: \(\tan \alpha = \tan \widehat {AOC} = \frac{{CA}}{{CO}} = \frac{3}{4}\).
Bài 2 trang 102 Vở thực hành Toán 9 thuộc chương trình học Toán 9, thường liên quan đến các kiến thức về hàm số bậc nhất, hệ số góc, đường thẳng song song và vuông góc. Việc nắm vững kiến thức nền tảng là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài 2 trang 102 VTH Toán 9 sẽ yêu cầu:
Để giải bài 2 trang 102 VTH Toán 9, chúng ta có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng phần của bài 2, tùy thuộc vào nội dung cụ thể của bài tập. Ví dụ:)
Ví dụ: Cho đường thẳng y = 2x - 3. Hãy xác định hệ số góc của đường thẳng này.
Lời giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
Khi giải bài tập về hàm số bậc nhất, bạn cần lưu ý:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 2 trang 102 Vở thực hành Toán 9. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình đường thẳng |
| a | Hệ số góc |
| a1 = a2 | Điều kiện hai đường thẳng song song |
| a1 * a2 = -1 | Điều kiện hai đường thẳng vuông góc |