Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Trang này tập trung vào việc giải các câu hỏi trắc nghiệm trang 33 trong Vở thực hành Toán 9 tập 2, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, dễ hiểu, kèm theo các giải thích rõ ràng để bạn có thể hiểu rõ bản chất của từng bài toán.
Điểm nào sau đây thuộc đồ thị của hàm số (y = frac{1}{2}{x^2})? A. (left( {1;2} right)). B. (left( {2;1} right)). C. (left( {2;1} right)). D. (left( { - 1;frac{1}{2}} right)).
Trả lời Câu 1 trang 33 Vở thực hành Toán 9
Điểm nào sau đây thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?
A. \(\left( {1;2} \right)\).
B. \(\left( {2;1} \right)\).
C. \(\left( {2;1} \right)\).
D. \(\left( { - 1;\frac{1}{2}} \right)\).
Phương pháp giải:
Thay \(x = - 1\) vào đồ thị hàm số \(y = \frac{1}{2}{x^2}\), tìm được \(y = \frac{1}{2}\) nên tìm được điểm thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Lời giải chi tiết:
Với \(x = - 1\), thay vào hàm số \(y = \frac{1}{2}{x^2}\) ta có: \(y = \frac{1}{2}.{\left( { - 1} \right)^2} = \frac{1}{2}\). Do đó, điểm \(\left( { - 1;\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Chọn D
Trả lời Câu 4 trang 33 Vở thực hành Toán 9
Phương trình bậc hai có hai nghiệm \({x_1} = 13\) và \({x_2} = 25\) là
A. \({x^2} - 13x + 25 = 0\).
B. \({x^2} - 25x + 13 = 0\).
C. \({x^2} - 38x + 325 = 0\).
D. \({x^2} + 38x + 325 = 0\).
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).
Lời giải chi tiết:
Tổng hai nghiệm của phương trình là \(S = 38,\) tích hai nghiệm của phương trình là \(P = 325\) nên \({x_1},{x_2}\) là hai nghiệm của phương trình: \({x^2} - 38x + 325 = 0\).
Chọn C
Trả lời Câu 3 trang 33 Vở thực hành Toán 9
Các nghiệm của phương trình \({x^2} + 7x + 12 = 0\) là
A. \({x_1} = 3;{x_2} = 4\).
B. \({x_1} = - 3;{x_2} = - 4\).
C. \({x_1} = 3;{x_2} = - 4\).
D. \({x_1} = - 3;{x_2} = 4\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\).
+ Nếu \(\Delta = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\).
+ Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
Vì \(\Delta = {7^2} - 4.1.12 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 7 + 1}}{2} = - 3;{x_2} = \frac{{ - 7 - 1}}{2} = - 4\)
Chọn B
Trả lời Câu 5 trang 33 Vở thực hành Toán 9
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 5x + 6 = 0\). Khi đó giá trị của biểu thức \(A = x_1^2 + x_2^2\) là
A. 13.
B. 19.
C. 25.
D. 5.
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\).
+ Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì áp dụng định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\).
Biến đổi \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), từ đó thay \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\) để tính giá trị biểu thức.
Lời giải chi tiết:
Vì \(\Delta = {\left( { - 5} \right)^2} - 4.6 = 1 > 0\) nên phương trình có hai nghiệm phân biệt.
Theo định lí Viète ta có: \({x_1} + {x_2} = 5;{x_1}.{x_2} = 6\)
Ta có: \(A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {5^2} - 2.6 = 13\)
Chọn A
Trả lời Câu 6 trang 33 Vở thực hành Toán 9
Chiều dài và chiều rộng của hình chữ nhật có chu vi 20cm và diện tích \(24c{m^2}\) là
A. 5cm và 4cm.
B. 6cm và 4cm.
C. 8cm và 3cm.
D. 10cm và 2cm.
Phương pháp giải:
+ Chiều dài và chiều rộng là nghiệm của phương trình \({x^2} - 10x + 24 = 0\).
+ Sử dụng công thức nghiệm thu gọn để tìm x, từ đó kết luận.
Lời giải chi tiết:
Nửa chu vi hình chữ nhật là: \(20:2 = 10\left( {cm} \right)\)
Chiều dài và chiều rộng là nghiệm của phương trình: \({x^2} - 10x + 24 = 0\)
Vì \(\Delta ' = {\left( { - 5} \right)^2} - 24 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = 5 + 1 = 6;{x_2} = 5 - 1 = 4\).
Do đó, chiều dài và chiều rộng của hình chữ nhật lần lượt là 6cm và 4cm (do chiều dài > chiều rộng).
Chọn B
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 33 Vở thực hành Toán 9
Điểm nào sau đây thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?
A. \(\left( {1;2} \right)\).
B. \(\left( {2;1} \right)\).
C. \(\left( {2;1} \right)\).
D. \(\left( { - 1;\frac{1}{2}} \right)\).
Phương pháp giải:
Thay \(x = - 1\) vào đồ thị hàm số \(y = \frac{1}{2}{x^2}\), tìm được \(y = \frac{1}{2}\) nên tìm được điểm thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Lời giải chi tiết:
Với \(x = - 1\), thay vào hàm số \(y = \frac{1}{2}{x^2}\) ta có: \(y = \frac{1}{2}.{\left( { - 1} \right)^2} = \frac{1}{2}\). Do đó, điểm \(\left( { - 1;\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Chọn D
Trả lời Câu 2 trang 33 Vở thực hành Toán 9
Hình bên là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?
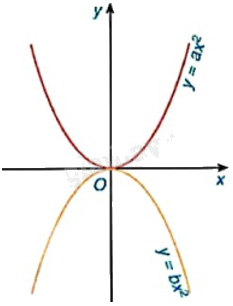
A. \(a < 0 < b\).
B. \(a < b < 0\).
C. \(a > b > 0\).
D. \(a > 0 > b\).
Phương pháp giải:
Đồ thị hàm số: \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Nằm phía trên trục hoành nếu \(a > 0\).
+ Nằm phía dưới trục hoành nếu \(a < 0\).
Lời giải chi tiết:
Vì đồ thị hàm số \(y = b{x^2}\) nằm phía dưới trục hoành nên \(0 > b\).
Vì đồ thị hàm số \(y = a{x^2}\) nằm phía trên trục hoành nên \(a > 0\).
Do đó, \(a > 0 > b\).
Chọn D
Trả lời Câu 3 trang 33 Vở thực hành Toán 9
Các nghiệm của phương trình \({x^2} + 7x + 12 = 0\) là
A. \({x_1} = 3;{x_2} = 4\).
B. \({x_1} = - 3;{x_2} = - 4\).
C. \({x_1} = 3;{x_2} = - 4\).
D. \({x_1} = - 3;{x_2} = 4\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\).
+ Nếu \(\Delta = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\).
+ Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
Vì \(\Delta = {7^2} - 4.1.12 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 7 + 1}}{2} = - 3;{x_2} = \frac{{ - 7 - 1}}{2} = - 4\)
Chọn B
Trả lời Câu 4 trang 33 Vở thực hành Toán 9
Phương trình bậc hai có hai nghiệm \({x_1} = 13\) và \({x_2} = 25\) là
A. \({x^2} - 13x + 25 = 0\).
B. \({x^2} - 25x + 13 = 0\).
C. \({x^2} - 38x + 325 = 0\).
D. \({x^2} + 38x + 325 = 0\).
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).
Lời giải chi tiết:
Tổng hai nghiệm của phương trình là \(S = 38,\) tích hai nghiệm của phương trình là \(P = 325\) nên \({x_1},{x_2}\) là hai nghiệm của phương trình: \({x^2} - 38x + 325 = 0\).
Chọn C
Trả lời Câu 5 trang 33 Vở thực hành Toán 9
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 5x + 6 = 0\). Khi đó giá trị của biểu thức \(A = x_1^2 + x_2^2\) là
A. 13.
B. 19.
C. 25.
D. 5.
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\).
+ Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì áp dụng định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\).
Biến đổi \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), từ đó thay \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\) để tính giá trị biểu thức.
Lời giải chi tiết:
Vì \(\Delta = {\left( { - 5} \right)^2} - 4.6 = 1 > 0\) nên phương trình có hai nghiệm phân biệt.
Theo định lí Viète ta có: \({x_1} + {x_2} = 5;{x_1}.{x_2} = 6\)
Ta có: \(A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {5^2} - 2.6 = 13\)
Chọn A
Trả lời Câu 6 trang 33 Vở thực hành Toán 9
Chiều dài và chiều rộng của hình chữ nhật có chu vi 20cm và diện tích \(24c{m^2}\) là
A. 5cm và 4cm.
B. 6cm và 4cm.
C. 8cm và 3cm.
D. 10cm và 2cm.
Phương pháp giải:
+ Chiều dài và chiều rộng là nghiệm của phương trình \({x^2} - 10x + 24 = 0\).
+ Sử dụng công thức nghiệm thu gọn để tìm x, từ đó kết luận.
Lời giải chi tiết:
Nửa chu vi hình chữ nhật là: \(20:2 = 10\left( {cm} \right)\)
Chiều dài và chiều rộng là nghiệm của phương trình: \({x^2} - 10x + 24 = 0\)
Vì \(\Delta ' = {\left( { - 5} \right)^2} - 24 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = 5 + 1 = 6;{x_2} = 5 - 1 = 4\).
Do đó, chiều dài và chiều rộng của hình chữ nhật lần lượt là 6cm và 4cm (do chiều dài > chiều rộng).
Chọn B
Trả lời Câu 2 trang 33 Vở thực hành Toán 9
Hình bên là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?
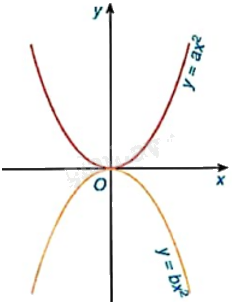
A. \(a < 0 < b\).
B. \(a < b < 0\).
C. \(a > b > 0\).
D. \(a > 0 > b\).
Phương pháp giải:
Đồ thị hàm số: \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Nằm phía trên trục hoành nếu \(a > 0\).
+ Nằm phía dưới trục hoành nếu \(a < 0\).
Lời giải chi tiết:
Vì đồ thị hàm số \(y = b{x^2}\) nằm phía dưới trục hoành nên \(0 > b\).
Vì đồ thị hàm số \(y = a{x^2}\) nằm phía trên trục hoành nên \(a > 0\).
Do đó, \(a > 0 > b\).
Chọn D
Trang 33 Vở thực hành Toán 9 tập 2 thường chứa các câu hỏi trắc nghiệm liên quan đến các chủ đề đã học trong chương. Các câu hỏi này có thể bao gồm các dạng bài tập về hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, phương trình bậc hai một ẩn, và các ứng dụng thực tế của đại số. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là rất quan trọng để đạt kết quả tốt trong các bài kiểm tra và kỳ thi.
Các câu hỏi trắc nghiệm trang 33 Vở thực hành Toán 9 tập 2 thường xuất hiện dưới các dạng sau:
Dưới đây là hướng dẫn giải chi tiết từng câu hỏi trắc nghiệm trang 33 Vở thực hành Toán 9 tập 2:
Cho hàm số y = 2x - 3. Hệ số a của hàm số là?
Lời giải:
Hàm số y = 2x - 3 có dạng y = ax + b, trong đó a = 2 và b = -3. Vậy hệ số a của hàm số là 2.
Nghiệm của hệ phương trình x + y = 5 x - y = 1 là?
Lời giải:
Cộng hai phương trình lại, ta được: 2x = 6 => x = 3. Thay x = 3 vào phương trình x + y = 5, ta được: 3 + y = 5 => y = 2. Vậy nghiệm của hệ phương trình là (x; y) = (3; 2).
Phương trình x2 - 5x + 6 = 0 có nghiệm là?
Lời giải:
Ta có a = 1, b = -5, c = 6. Tính delta: Δ = b2 - 4ac = (-5)2 - 4 * 1 * 6 = 25 - 24 = 1. Vì Δ > 0, phương trình có hai nghiệm phân biệt: x1 = (-b + √Δ) / 2a = (5 + 1) / 2 = 3 và x2 = (-b - √Δ) / 2a = (5 - 1) / 2 = 2. Vậy phương trình có nghiệm x1 = 3 và x2 = 2.
Để giải nhanh các bài tập trắc nghiệm Toán 9, bạn có thể áp dụng một số mẹo sau:
Việc luyện tập thường xuyên là yếu tố then chốt để nắm vững kiến thức và kỹ năng giải bài tập Toán 9. Bạn nên dành thời gian giải các bài tập trong sách giáo khoa, vở thực hành, và các đề thi thử để làm quen với các dạng bài tập khác nhau và rèn luyện khả năng giải quyết vấn đề.
Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải nhanh trên, bạn sẽ tự tin hơn trong việc giải các câu hỏi trắc nghiệm trang 33 Vở thực hành Toán 9 tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!