Bài 2 trang 35 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 2 trang 35 VTH Toán 9 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hàm số (y = a{x^2}). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó.
Đề bài
Cho hàm số \(y = a{x^2}\). Xác định hệ số a, biết đồ thị hàm số đi qua điểm A(3; 3). Vẽ đồ thị của hàm số trong trường hợp đó.
Phương pháp giải - Xem chi tiết
- Thay \(x = 3;y = 3\) vào hàm số \(y = a{x^2}\) để tìm a.
- Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải chi tiết
Thay \(x = 3\) và \(y = 3\) vào phương trình \(y = a{x^2}\)ta có: \(3 = a{.3^2}\), suy ra \(a = \frac{1}{3}\).
Lập bảng một số giá trị tương ứng giữa x và \(y = \frac{1}{3}{x^2}\).

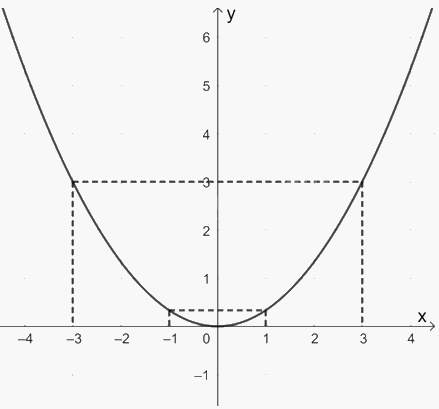
Đồ thị của hàm số \(y = \frac{1}{3}{x^2}\) như hình sau:
Bài 2 trang 35 Vở thực hành Toán 9 tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 2 trang 35 VTH Toán 9 tập 2, học sinh thường được yêu cầu:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Để xác định hàm số bậc nhất, học sinh cần tìm được các hệ số a và b trong công thức y = ax + b. Dựa vào các điều kiện cho trước trong đề bài, học sinh có thể sử dụng phương pháp thay thế hoặc giải hệ phương trình để tìm ra giá trị của a và b.
Sau khi xác định được hàm số bậc nhất, học sinh có thể vẽ đồ thị của hàm số bằng cách:
Để tìm tọa độ giao điểm của đồ thị hàm số với các đường thẳng khác, học sinh cần giải hệ phương trình gồm phương trình của hàm số và phương trình của đường thẳng đó. Nghiệm của hệ phương trình chính là tọa độ giao điểm.
Ngoài bài 2 trang 35 VTH Toán 9 tập 2, còn rất nhiều bài tập tương tự liên quan đến hàm số bậc nhất. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để đạt được kết quả tốt nhất khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý những điều sau:
Bài 2 trang 35 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Đồ thị hàm số bậc nhất | Đường thẳng đi qua hai điểm bất kỳ trên đồ thị. |
| Hệ số góc | Hệ số a trong công thức y = ax + b. |