Bạn đang gặp khó khăn trong việc giải các bài tập trắc nghiệm Toán 9 tập 2, cụ thể là trang 39 và 40 của Vở thực hành? Đừng lo lắng, giaitoan.edu.vn sẽ đồng hành cùng bạn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong các bài kiểm tra.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho bạn những giải pháp tối ưu nhất.
Điểm thi môn Toán của 35 học sinh lớp 9D được cho trong bảng sau: Giá trị của x là: A. 15. B. 16. C. 17. D. 18.
Trả lời Câu 2 trang 40 Vở thực hành Toán 9
Bạn Nam ghi lại số môn thể thao mà các bạn trong tổ có thể chơi được cho kết quả như sau:
2, 4, 3, 2, 1, 2, 3, 2, 3, 1.
Tần số của giá trị 2 là:
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp giải:
Tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu.
Lời giải chi tiết:
Vì giá trị 2 xuất hiện 4 lần nên giá trị 2 có tần số là 4.
Chọn D
Trả lời Câu 4 trang 40 Vở thực hành Toán 9
Tần số m của một giá trị trong mẫu số liệu
A. có thể là số vô tỉ.
B. có thể là số nguyên âm.
C. phải là số tự nhiên.
D. không nhất thiết là số tự nhiên.
Phương pháp giải:
Tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu.
Lời giải chi tiết:
Vì tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu nên tần số m của một giá trị trong mẫu số liệu phải là số tự nhiên.
Chọn C
Trả lời Câu 3 trang 40 Vở thực hành Toán 9
Cho bảng số liệu về kết quả đánh giá của các bạn học sinh lớp 9A về công tác tổ chức trại hè của Đoàn thanh niên trường nhân dịp Tết trung thu:

Không thể dùng biểu đồ nào sau đây để biểu diễn bảng thống kê trên?
A. Biểu đồ tranh.
B. Biểu đồ đoạn thẳng.
C. Biểu đồ tần số dạng cột.
D. Biểu đồ tần số dạng đoạn thẳng.
Phương pháp giải:
Biểu đồ đoạn thẳng không thể dùng để biểu diễn bảng thống kê trên.
Lời giải chi tiết:
Biểu đồ đoạn thẳng không thể dùng để biểu diễn bảng thống kê trên.
Chọn B
Trả lời Câu 1 trang 39 Vở thực hành Toán 9
Điểm thi môn Toán của 35 học sinh lớp 9D được cho trong bảng sau:

Giá trị của x là:
A. 15.
B. 16.
C. 17.
D. 18.
Phương pháp giải:
Bảng tần số có dạng bảng sau:
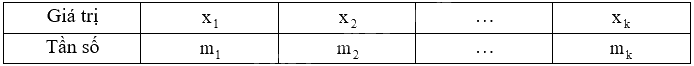
Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
Lời giải chi tiết:
Ta có: \(2 + x + 10 + 6 = 35\) nên \(x = 17\).
Chọn C
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 39 Vở thực hành Toán 9
Điểm thi môn Toán của 35 học sinh lớp 9D được cho trong bảng sau:

Giá trị của x là:
A. 15.
B. 16.
C. 17.
D. 18.
Phương pháp giải:
Bảng tần số có dạng bảng sau:
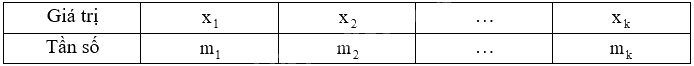
Trong đó, \({m_1}\) là tần số của \({x_1}\), \({m_2}\) là tần số của \({x_2}\),…, \({m_k}\) là tần số của \({x_k}\).
Lời giải chi tiết:
Ta có: \(2 + x + 10 + 6 = 35\) nên \(x = 17\).
Chọn C
Trả lời Câu 2 trang 40 Vở thực hành Toán 9
Bạn Nam ghi lại số môn thể thao mà các bạn trong tổ có thể chơi được cho kết quả như sau:
2, 4, 3, 2, 1, 2, 3, 2, 3, 1.
Tần số của giá trị 2 là:
A. 1.
B. 2.
C. 3.
D. 4.
Phương pháp giải:
Tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu.
Lời giải chi tiết:
Vì giá trị 2 xuất hiện 4 lần nên giá trị 2 có tần số là 4.
Chọn D
Trả lời Câu 3 trang 40 Vở thực hành Toán 9
Cho bảng số liệu về kết quả đánh giá của các bạn học sinh lớp 9A về công tác tổ chức trại hè của Đoàn thanh niên trường nhân dịp Tết trung thu:

Không thể dùng biểu đồ nào sau đây để biểu diễn bảng thống kê trên?
A. Biểu đồ tranh.
B. Biểu đồ đoạn thẳng.
C. Biểu đồ tần số dạng cột.
D. Biểu đồ tần số dạng đoạn thẳng.
Phương pháp giải:
Biểu đồ đoạn thẳng không thể dùng để biểu diễn bảng thống kê trên.
Lời giải chi tiết:
Biểu đồ đoạn thẳng không thể dùng để biểu diễn bảng thống kê trên.
Chọn B
Trả lời Câu 4 trang 40 Vở thực hành Toán 9
Tần số m của một giá trị trong mẫu số liệu
A. có thể là số vô tỉ.
B. có thể là số nguyên âm.
C. phải là số tự nhiên.
D. không nhất thiết là số tự nhiên.
Phương pháp giải:
Tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu.
Lời giải chi tiết:
Vì tần số của một giá trị là số lần xuất hiện của giá trị đó trong mẫu dữ liệu nên tần số m của một giá trị trong mẫu số liệu phải là số tự nhiên.
Chọn C
Trang 39 và 40 của Vở thực hành Toán 9 tập 2 thường tập trung vào các chủ đề như hàm số bậc nhất, hệ số góc, đường thẳng song song và vuông góc. Các bài tập trắc nghiệm ở đây đòi hỏi học sinh phải nắm vững định nghĩa, tính chất và các công thức liên quan. Việc giải đúng các bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề.
Để giải câu hỏi này, học sinh cần nhớ lại định nghĩa về hệ số góc của đường thẳng. Hệ số góc của đường thẳng y = ax + b là a. Do đó, học sinh chỉ cần xác định hệ số a trong phương trình đường thẳng đã cho là có thể tìm ra đáp án.
Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc. Do đó, học sinh cần tìm đường thẳng có hệ số góc bằng 2.
Hai đường thẳng vuông góc khi và chỉ khi tích hệ số góc của chúng bằng -1. Do đó, học sinh cần tìm đường thẳng có hệ số góc là nghịch đảo của -1, tức là 1.
Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình bậc nhất hai ẩn tạo bởi hai phương trình đường thẳng. Nghiệm của hệ phương trình chính là tọa độ giao điểm.
Để giải câu hỏi này, học sinh cần thay tọa độ của điểm A vào phương trình đường thẳng và giải phương trình để tìm giá trị của m.
Ví dụ: Cho đường thẳng y = 3x - 2. Xác định hệ số góc của đường thẳng này.
Giải: Hệ số góc của đường thẳng y = 3x - 2 là 3.
Để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa, sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với các mức độ khó khác nhau để bạn có thể nâng cao khả năng của mình.
Giải bài tập trắc nghiệm không chỉ giúp bạn củng cố kiến thức mà còn giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài thi nhanh chóng và chính xác. Đây là một kỹ năng quan trọng để đạt kết quả tốt trong các kỳ thi.
Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải các câu hỏi trắc nghiệm trang 39, 40 Vở thực hành Toán 9 tập 2. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất. Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.