Giải bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2

Giải bài 2 trang 103, 104 vở thực hành Toán 9 tập 2

Giải bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.

Trong các hình dưới đây, hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều ({60^o}) tâm O biến điểm M thành điểm N?

Đề bài

Trong các hình dưới đây, hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều \({60^o}\) tâm O biến điểm M thành điểm N?

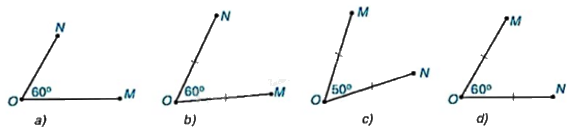
Giải bài 2 trang 103, 104 vở thực hành Toán 9 tập 2 1

Phương pháp giải - Xem chi tiết Giải bài 2 trang 103, 104 vở thực hành Toán 9 tập 2 2

Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).

Lời giải chi tiết

Hình d biểu diễn phép quay thuận chiều 60^o tâm O biến điểm M thành điểm N.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 2 trang 103, 104 vở thực hành Toán 9 tập 2 đặc sắc thuộc chuyên mục toán 9 sgk trên nền tảng toán học. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2: Hướng dẫn chi tiết và dễ hiểu

Bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, giúp các em hiểu sâu hơn về ứng dụng của hàm số bậc nhất trong đời sống.

Phần 1: Tóm tắt lý thuyết cần nắm vững

Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:

Hàm số bậc nhất: Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Đồ thị hàm số bậc nhất: Đồ thị hàm số bậc nhất là một đường thẳng.
Hệ số góc a: Hệ số a xác định độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải.
Giao điểm với trục Oy: Giao điểm của đồ thị hàm số với trục Oy là điểm có tọa độ (0, b).
Giao điểm với trục Ox: Giao điểm của đồ thị hàm số với trục Ox là điểm có tọa độ (-b/a, 0).

Phần 2: Giải chi tiết bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2

Để giải bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2, chúng ta cần phân tích kỹ đề bài và xác định các yếu tố quan trọng. Thông thường, bài tập này sẽ yêu cầu chúng ta:

Xác định hàm số bậc nhất dựa trên các thông tin đã cho.
Vẽ đồ thị hàm số bậc nhất.
Tìm tọa độ giao điểm của đồ thị hàm số với các trục tọa độ.
Giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất.

Ví dụ minh họa:

Giả sử đề bài yêu cầu chúng ta tìm hàm số bậc nhất đi qua hai điểm A(1, 2) và B(2, 5). Chúng ta có thể giải bài toán này như sau:

Bước 1: Xác định hệ số góc a. Ta có a = (y₂ - y₁) / (x₂ - x₁) = (5 - 2) / (2 - 1) = 3.
Bước 2: Xác định hệ số b. Ta có y = ax + b, thay điểm A(1, 2) vào, ta được 2 = 3 * 1 + b, suy ra b = -1.
Bước 3: Vậy hàm số bậc nhất cần tìm là y = 3x - 1.

Sau khi xác định được hàm số, chúng ta có thể vẽ đồ thị hàm số và tìm tọa độ giao điểm với các trục tọa độ.

Phần 3: Luyện tập thêm các bài tập tương tự

Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, bạn có thể luyện tập thêm các bài tập tương tự trong Vở thực hành Toán 9 tập 2 và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.

Phần 4: Mẹo giải bài tập hàm số bậc nhất hiệu quả

Để giải bài tập hàm số bậc nhất hiệu quả, bạn có thể áp dụng một số mẹo sau:

Đọc kỹ đề bài và xác định các yếu tố quan trọng.
Vẽ đồ thị hàm số để hình dung rõ hơn về bài toán.
Sử dụng các công thức và định lý đã học để giải quyết bài toán.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Phần 5: Tổng kết

Bài 2 trang 103, 104 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết và dễ hiểu trên đây, bạn đã có thể giải bài tập này một cách hiệu quả. Chúc bạn học tốt!