Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 6 trang 110, 111 Vở thực hành Toán 9. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã trình bày lời giải một cách rõ ràng, từng bước, kèm theo các giải thích chi tiết để bạn có thể hiểu rõ bản chất của bài toán.
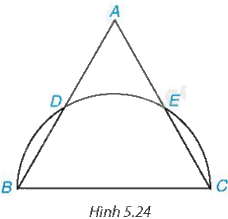
Cho tam giác đều ABC có (AB = 2sqrt 3 cm). Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C). (H.5.24). a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy. b) Tính diện tích của hình viên phân giới hạn bởi dây BD và cung nhỏ BD.
Đề bài
Cho tam giác đều ABC có \(AB = 2\sqrt 3 cm\). Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C). (H.5.24).
a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.
b) Tính diện tích của hình viên phân giới hạn bởi dây BD và cung nhỏ BD.
Phương pháp giải - Xem chi tiết
a) Gọi O là trung điểm của BC.
+ Chứng minh CD, BE là đường cao của tam giác đều ABC, từ đó suy ra D, E lần lượt là trung điểm của AB, AC.
+ Chứng minh các tam giác BOD, DOE, EOC là các tam giác đều, suy ra số đo các góc BOD, DOE, EOC.
+ Ba cung nhỏ $\overset\frown{BD},\overset\frown{DE}$ và $\overset\frown{EC}$ lần lượt bị chắn bởi các góc ở tâm BOD, DOE, EOC nên tính được số đo các cung đó.
b) Diện tích hình viên phân bằng diện tích hình quạt tròn ứng với cung BD trừ đi diện tích tam giác BOD.
Lời giải chi tiết
(H.5.25)
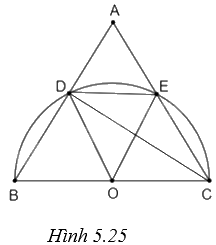
a) Gọi O là trung điểm của BC. Tam giác DBC có đường trung tuyến DO bằng \(\frac{1}{2}BC\) (bằng một nửa cạnh huyền) nên DBC là tam giác vuông tại D. Vậy CD là đường cao của tam giác đều ABC, suy ra D là trung điểm của AB. Tương tự, E là trung điểm của AC. Từ đó suy ra bốn tam giác BOD, DOE, EOC, ADE là những tam giác đều, với độ dài cạnh bằng một nửa độ dài cạnh của tam giác đều ABC, tức là bằng \(\sqrt 3 cm\).
Ba cung nhỏ $\overset\frown{BD},\overset\frown{DE}$ và $\overset\frown{EC}$ lần lượt bị chắn bởi các góc ở tâm BOD, DOE, EOC, mà có góc này đều bằng 60 độ (các góc của tam giác đều) nên các cung đang xét có số đo bằng nhau và cùng có số đo bằng 60 độ.
b) Diện tích hình quạt tròn ứng với cung BD là: \({S_q} = \frac{{60}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \frac{\pi }{2}\left( {c{m^2}} \right)\)
Diện tích của tam giác BOD là: \({S_{BOD}} = \frac{1}{2}{\left( {\sqrt 3 } \right)^2}\sin {60^o} = \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Diện tích hình viên phân là: \(S = {S_q} - {S_{BOD}} = \frac{\pi }{2} - \frac{{3\sqrt 3 }}{4} = \frac{{2\pi - 3\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Bài 6 trang 110, 111 Vở thực hành Toán 9 thuộc chương trình học Toán 9, thường liên quan đến các kiến thức về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các phương pháp giải toán liên quan.
Trước khi đi vào giải bài tập cụ thể, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 6 trang 110, 111 Vở thực hành Toán 9, chúng ta cần phân tích đề bài và xác định các yếu tố quan trọng. Dưới đây là hướng dẫn giải chi tiết cho từng phần của bài tập:
Đề bài yêu cầu xác định hàm số bậc nhất dựa trên các thông tin cho trước. Để làm điều này, chúng ta cần sử dụng các công thức và phương pháp đã học để tìm ra hệ số a và b.
Ví dụ, nếu đề bài cho hai điểm mà đường thẳng đi qua, chúng ta có thể sử dụng công thức tính hệ số góc: a = (y2 - y1) / (x2 - x1). Sau đó, sử dụng một trong hai điểm và hệ số góc để tìm ra hệ số b.
Sau khi xác định được hàm số, chúng ta cần vẽ đồ thị của hàm số trên mặt phẳng tọa độ. Để vẽ đồ thị, chúng ta có thể chọn một vài điểm thuộc đồ thị và nối chúng lại với nhau. Lưu ý rằng đồ thị của hàm số bậc nhất là một đường thẳng.
Nếu đề bài yêu cầu tìm giao điểm của hai đường thẳng, chúng ta cần giải hệ phương trình bậc nhất hai ẩn. Giao điểm của hai đường thẳng là nghiệm của hệ phương trình.
Để củng cố kiến thức và kỹ năng giải toán, bạn có thể làm thêm các bài tập tương tự trong Vở thực hành Toán 9 và các tài liệu tham khảo khác. Dưới đây là một số bài tập gợi ý:
Để học Toán 9 hiệu quả, bạn nên:
Bài 6 trang 110, 111 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng của hàm số trong thực tế. Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong các bài kiểm tra.