Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 82, 83 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau: E: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 11”; F: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 hoặc 9”; G: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 6”.
Đề bài
Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:
E: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 11”;
F: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 hoặc 9”;
G: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 6”.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
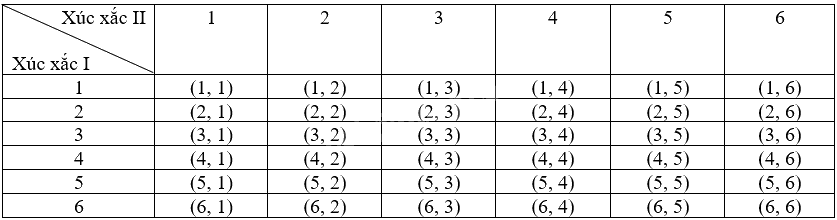
Mỗi ô ở bảng trên là một kết quả có thể. Có 36 kết quả có thể là đồng khả năng.
- Có 2 kết quả thuận lợi cho biến cố E là: (5, 6), (6, 5).
Vậy \(P\left( E \right) = \frac{2}{{36}} = \frac{1}{{18}}\).
- Tổng số chấm bằng 8 là các ô (2, 6); (3, 5); (4, 4); (5, 3); (6, 2).
Tổng số chấm bằng 9 là các ô (3, 6); (4, 5); (5, 4); (6, 3).
Có 9 kết quả thuận lợi cho biến cố F là (2, 6); (3, 5); (4, 4); (5, 3); (6, 2); (3, 6); (4, 5); (5, 4); (6, 3).
Vậy \(P\left( F \right) = \frac{9}{{36}} = \frac{1}{4}\).
- Tổng số chấm bằng 5 là các ô (1, 4); (2, 3); (3, 2); (4, 1).
Tổng số chấm bằng 4 là các ô (1, 3); (2, 2); (3, 1).
Tổng số chấm bằng 3 là các ô (1, 2); (2, 1).
Tổng số chấm bằng 2 là ô (1, 1).
Có 10 kết quả thuận lợi của biến cố G là (1, 4); (2, 3); (3, 2); (4, 1); (1, 3); (2, 2); (3, 1); (1, 2); (2, 1); (1, 1).
Vậy \(P\left( G \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).
Bài 2 trang 82, 83 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định các yếu tố của hàm số, vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất.
Bài 2 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Ví dụ 1: Cho hàm số y = 2x + b. Biết rằng đồ thị hàm số đi qua điểm A(1; 3). Hãy tìm giá trị của b.
Giải: Vì đồ thị hàm số đi qua điểm A(1; 3) nên tọa độ của điểm A thỏa mãn phương trình của hàm số. Thay x = 1 và y = 3 vào phương trình y = 2x + b, ta được:
3 = 2 * 1 + b
=> b = 3 - 2 = 1
Vậy, b = 1.
Ví dụ 2: Vẽ đồ thị hàm số y = -x + 2.
Giải:
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý các điểm sau:
Để củng cố kiến thức về bài 2 trang 82, 83 Vở thực hành Toán 9 tập 2, các em có thể tự giải các bài tập sau:
Bài 2 trang 82, 83 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ học tập tốt môn Toán 9.