Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 92 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em giải quyết mọi khó khăn trong môn Toán.
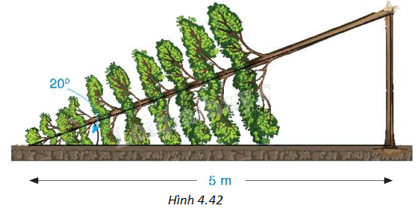
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc ({20^o}) và chắn ngang lối đi một đoạn 5m (H.4.42). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Đề bài
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc \({20^o}\) và chắn ngang lối đi một đoạn 5m (H.4.42). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
+ Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.
+ Trong tam giác ABC vuông tại A, ta có: \(AB = AC.\tan C\) tính được AB, \(\cos \widehat {ACB} = \frac{{AC}}{{BC}}\) tính được CB.
+ Chiều cao của cây trước khi đổ gãy là: \(AB + BC\).
Lời giải chi tiết
(H.4.43)
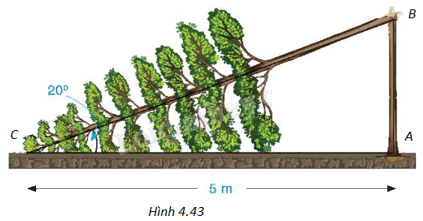
Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.
Trong tam giác ABC vuông tại A, ta có \(AB = AC.\tan C = 5.\tan {20^o}\), \(\cos \widehat {ACB} = \frac{{AC}}{{BC}} = \frac{5}{{CB}}\) nên \(BC = \frac{5}{{\cos {{20}^o}}}\).
Do đó, chiều cao của cây trước khi đổ gãy là
\(AB + BC = 5.\tan {20^o} + \frac{5}{{\cos {{20}^o}}} \\= 5\left( {\tan {{20}^o} + \frac{1}{{\cos {{20}^o}}}} \right) \approx 7,1\left( m \right)\)
Bài 4 trang 92 Vở thực hành Toán 9 thuộc chương trình học Toán lớp 9, thường liên quan đến các kiến thức về hàm số bậc nhất, đồ thị hàm số, hoặc các ứng dụng của hàm số trong thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan.
Tùy thuộc vào từng phiên bản Vở thực hành Toán 9, nội dung bài 4 có thể khác nhau. Tuy nhiên, thường gặp các dạng bài tập sau:
Để giải bài 4 trang 92 Vở thực hành Toán 9 một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Cho hàm số y = 2x + 1. Hãy tìm tọa độ giao điểm của đồ thị hàm số với trục Ox.
Giải:
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Ox, ta cần giải phương trình y = 0:
2x + 1 = 0
=> 2x = -1
=> x = -1/2
Vậy tọa độ giao điểm của đồ thị hàm số với trục Ox là (-1/2, 0).
Khi giải bài 4 trang 92 Vở thực hành Toán 9, học sinh cần lưu ý những điều sau:
Để học tập và ôn luyện môn Toán 9 hiệu quả, học sinh có thể tham khảo các tài liệu sau:
Bài 4 trang 92 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và ứng dụng của hàm số trong thực tế. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.