Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 4 trang 109 Vở thực hành Toán 9 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho đường tròn (O; 5cm). a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5cm. b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm). c) Tính số đo và độ dài của cung nhỏ AB. d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Đề bài
Cho đường tròn (O; 5cm).
a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5cm.
b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm).
c) Tính số đo và độ dài của cung nhỏ AB.
d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Phương pháp giải - Xem chi tiết
a) - Lấy điểm I tùy ý sao cho \(OI = 2,5cm\);
- Vẽ đường thẳng vuông góc với OI tại I, cắt (O) tại A và B. Ta có dây AB cần vẽ.
b) + Kéo dài OI cắt (O) tại K.
+ Chứng minh tứ giác AOBK là hình thoi, suy ra \(OA = OK = KA\)
+ Chứng minh tam giác OAK đều, từ đó tính được góc AOK và góc OAB.
+ \(sđ\overset\frown{AB}=\widehat{AOK}\) từ đó tính được số đo cung nhỏ AB.
c) Độ dài l của cung \({n^o}\) trên đường tròn (O; R) là \(l = \frac{n}{{180}}.\pi R\).
d) Diện tích \({S_q}\) của hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{n}{{360}}.\pi {R^2}\).
Lời giải chi tiết
a) Vẽ dây AB cách O một khoảng 2,5cm:
- Lấy điểm I tùy ý sao cho \(OI = 2,5cm\);
- Vẽ đường thẳng vuông góc với OI tại I, cắt (O) tại A và B. Ta có dây AB cần vẽ:
b) (H.5.22)
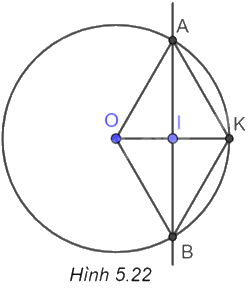
Trong tam giác vuông AOI, ta có \(A{I^2} = O{A^2} - O{I^2} = {5^2} - {2,5^2} = 18,75\).
Vậy \(AB = 2AI = 2\sqrt {18,75} \approx 8,66\left( {cm} \right)\)
c) (H.5.22)
Kéo dài OI cắt (O) tại K.
Dễ thấy tứ giác AKBO có hai đường chéo AB và OK vuông góc với nhau và cắt nhau tại trung điểm mỗi đường (do \(AI = IB\) và \(OI = IK = \frac{{OK}}{2}\)).
Do đó AKBO là hình thoi.
Từ đó \(OA = OK = KA = 5cm\); OAK là tam giác đều, suy ra \(\widehat {AOK} = {60^o}\) và \(\widehat {AOB} = 2\widehat {AOK} = {120^o}\).
Vậy \(sđ\overset\frown{AB}=\widehat{AOK}={{120}^{o}}\).
Độ dài cung nhỏ AB bằng \(\frac{{120}}{{180}}\pi .5 = \frac{{10\pi }}{3}\left( {cm} \right)\).
d) Diện tích hình quạt tròn ứng với cung AB là:
\({S_q} = \frac{{120}}{{360}}.\pi {.5^2} = \frac{{25\pi }}{3}\left( {c{m^2}} \right)\).
Bài 4 trang 109 Vở thực hành Toán 9 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và tìm điều kiện để hàm số đồng biến hoặc nghịch biến. Việc nắm vững các khái niệm này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình Toán 9.
Bài 4 trang 109 Vở thực hành Toán 9 thường có dạng như sau:
Để giải bài 4 trang 109 Vở thực hành Toán 9, bạn có thể áp dụng các phương pháp sau:
Ví dụ 1: Cho hàm số y = 2x - 1. Tìm giá trị của y khi x = 3.
Giải: Thay x = 3 vào phương trình y = 2x - 1, ta được: y = 2 * 3 - 1 = 5. Vậy, khi x = 3 thì y = 5.
Ví dụ 2: Cho hàm số y = -x + 2. Tìm điều kiện của x để hàm số nghịch biến.
Giải: Hàm số y = -x + 2 là hàm số bậc nhất với a = -1. Vì a < 0, nên hàm số nghịch biến trên toàn bộ tập số thực.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 4 trang 109 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất. Bằng cách áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 9.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a > 0 | Hàm số đồng biến |
| a < 0 | Hàm số nghịch biến |