Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 94 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu, nhanh chóng và chính xác.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, giúp các em học Toán 9 hiệu quả hơn. Hãy cùng bắt đầu với bài giải bài 7 trang 94 nhé!
Đố vui. Chu vi Trái Đất bằng bao nhiêu? Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau: 1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng. 2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-l
Đề bài
Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
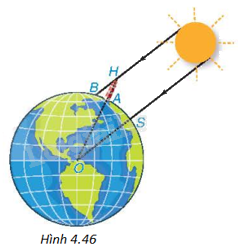
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.46, điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).
Phương pháp giải - Xem chi tiết
+ Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
+ Vì \(AH = 25m\) khá bé so với R, Earthostene coi cung tròn AB của (C) là một đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}}\) nên tính được góc SOA.
+ Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON}\), mà độ dài cung AS bằng 800km ứng với góc ở tâm \(\widehat {AOS} \approx {7^o}\) nên toàn bộ đường tròn (C) ứng với góc ở tâm \({360^o}\) có độ dài xấp xỉ bằng \(\frac{{360}}{7}.800\).
Lời giải chi tiết
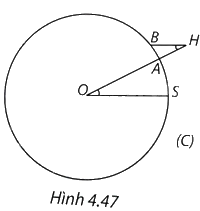
Trên Hình 4.47 đường tròn (C) với O là tâm Trái Đất, đi qua S (Syene), A (Alexandria), \(OS = OA = R\) (R là bán kính của đường tròn (C)).
Theo giả thiết, cung tròn (nhỏ) SA của (C) dài 800km.
Gọi H là đỉnh tháp, chân tại A thì A nằm giữa O và H, \(AH = 25m\). Bóng của tháp là cung tròn AB của (C).
Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
Vì \(AH = 25m\) khá bé so với R, Earthostene coi cung tròn AB của (C) là một đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}} = \frac{{3,1}}{{25}} = \frac{{31}}{{250}}\)
Suy ra \(\tan \widehat {AOS} = \frac{{31}}{{250}}\) nên \(\widehat {AOS} \approx {7^o}\)
Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON}\), mà độ dài cung AS bằng 800km ứng với góc ở tâm \(\widehat {AOS} \approx {7^o}\) nên toàn bộ đường tròn (C) ứng với góc ở tâm \({360^o}\) có độ dài xấp xỉ bằng \(\frac{{360}}{7}.800 \approx 41\;143\left( {km} \right)\).
Bài 7 trang 94 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, đường thẳng song song, và ứng dụng hàm số vào các bài toán hình học.
Bài 7 thường bao gồm các dạng bài tập sau:
Để giải bài 7 trang 94 Vở thực hành Toán 9 một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Ví dụ: Cho đường thẳng y = 2x - 1. Hãy xác định hệ số góc của đường thẳng này.
Giải: Dựa vào phương trình đường thẳng y = 2x - 1, ta thấy hệ số góc của đường thẳng là a = 2.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, học sinh nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập, và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Ngoài Vở thực hành Toán 9, học sinh có thể tham khảo thêm các tài liệu sau:
Để học Toán 9 hiệu quả, học sinh nên:
Bài 7 trang 94 Vở thực hành Toán 9 là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!