Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 80 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Tính các góc của hình thoi có hai đường chéo dài (2sqrt 3 ) và 2.
Đề bài
Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3 \) và 2.
Phương pháp giải - Xem chi tiết
+ Hình thoi ABCD có \(AC = 2\sqrt 3 ,BD = 2\) nên tính được AO, BO.
+ Tam giác AOB vuông tại O nên \(\tan \widehat {BAO} = \frac{{BO}}{{AO}}\) từ đó tính được góc BAO.
+ Vì ABCD là hình thoi nên \(\widehat {BAD} = 2\widehat {BAO}\), \(\widehat {ABC} = {180^o} - \widehat {BAD}\).
Lời giải chi tiết
(H.4.17)
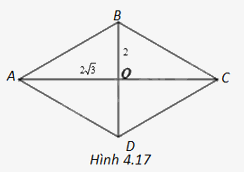
Hình thoi ABCD có \(AC = 2\sqrt 3 ,BD = 2\)
Ta có: \(AO = \frac{1}{2}AC = \sqrt 3 ,BO = \frac{1}{2}BD = \frac{1}{2}.2 = 1\)
Dễ thấy tam giác ABO vuông tại O.
Trong tam giác vuông ABO có \(\tan \widehat {BAO} = \frac{{BO}}{{AO}} = \frac{1}{{\sqrt 3 }}\), suy ra \(\widehat {BAO} = {30^o}\), do đó \(\widehat {BAD} = 2\widehat {BAO} = {2.30^o} = {60^o}\)
Do ABCD là hình thoi nên \(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {60^o} = {120^o}\)
Vậy hình thoi ABCD có một góc bằng 60 độ và góc kia bằng 120 độ.
Bài 4 trang 80 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị hàm số, và giải các phương trình, bất phương trình liên quan.
Để giải quyết bài 4 trang 80 Vở thực hành Toán 9 một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài 4 thường bao gồm nhiều câu hỏi nhỏ, mỗi câu hỏi yêu cầu học sinh áp dụng một kiến thức cụ thể. Dưới đây là hướng dẫn chi tiết cách giải từng câu hỏi:
Để xác định hệ số góc và tung độ gốc của hàm số, ta chỉ cần so sánh hàm số đã cho với dạng tổng quát y = ax + b (đối với hàm số bậc nhất) hoặc y = ax2 + bx + c (đối với hàm số bậc hai). Sau đó, ta đối chiếu các hệ số để tìm ra giá trị của a và b (hoặc a, b, c).
Để kiểm tra một điểm (x0, y0) thuộc đồ thị hàm số y = f(x), ta thay x0 vào hàm số để tính y. Nếu y = y0, thì điểm (x0, y0) thuộc đồ thị hàm số. Ngược lại, nếu y ≠ y0, thì điểm (x0, y0) không thuộc đồ thị hàm số.
Để giải phương trình hoặc bất phương trình, ta sử dụng các phương pháp đại số đã học, như phân tích thành nhân tử, sử dụng công thức nghiệm, hoặc biến đổi tương đương. Lưu ý, khi giải bất phương trình, ta cần đổi dấu bất phương trình khi nhân hoặc chia cả hai vế cho một số âm.
Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số. Kiểm tra xem điểm A(1, -1) có thuộc đồ thị hàm số hay không.
Giải:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Để học Toán 9 hiệu quả, các em cần:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 4 trang 80 Vở thực hành Toán 9 một cách hiệu quả. Chúc các em học tập tốt!