Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 131 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các bài tập luyện tập để nắm vững kiến thức.
Kí hiệu (left( {{d_1}} right)) là đường thẳng (x + 2y = 4,left( {{d_2}} right)) là đường thẳng (x - y = 1). a) Vẽ (left( {{d_1}} right)) và (left( {{d_2}} right)) trên cùng một mặt phẳng tọa độ. b) Giải hệ phương trình (left{ begin{array}{l}x + 2y = 4\x - y = 1end{array} right.) để tìm tọa độ giao điểm của hai đường thẳng (left( {{d_1}} right)) và (left( {{d_2}} right)).
Đề bài
Kí hiệu \(\left( {{d_1}} \right)\) là đường thẳng \(x + 2y = 4,\left( {{d_2}} \right)\) là đường thẳng \(x - y = 1\).
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ.
b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 4\\x - y = 1\end{array} \right.\) để tìm tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\).
Phương pháp giải - Xem chi tiết
a) Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right)\) và điểm \(B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {1;0} \right)\) và \(D\left( {0; - 1} \right)\).
Biểu diễn các điểm A, B, C, D trên cùng một mặt phẳng tọa độ Oxy.
b) Giải hệ phương trình bằng phương pháp thế.
Lời giải chi tiết
a) Nhận xét:
Đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(A\left( {0;2} \right)\) và điểm \(B\left( {4;0} \right)\).
Đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(C\left( {1;0} \right)\) và \(D\left( {0; - 1} \right)\).
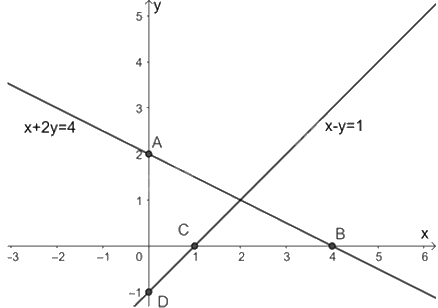
b) Xét hệ hai phương trình bậc nhất hai ẩn:
\(\left\{ \begin{array}{l}x + 2y = 4\\x - y = 1\end{array} \right.\) .
Từ phương trình thứ hai suy ra \(x = y + 1\). Thế vào phương trình thứ nhất ta được:
\(y + 1 + 2y = 4\), hay \(3y = 3\), suy ra \(y = 1\).
Từ đó tìm được \(x = 2\).
Vậy giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là điểm (2; 1).
Bài 5 trang 131 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình ôn tập về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số bậc nhất, bao gồm:
Bài 5 trang 131 Vở thực hành Toán 9 tập 2 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5 trang 131 Vở thực hành Toán 9 tập 2, chúng tôi xin trình bày lời giải chi tiết như sau:
Câu a: (Ví dụ về một câu a cụ thể, giả sử là xác định hàm số bậc nhất)
Cho hàm số y = 2x + 3. Hãy xác định đây có phải là hàm số bậc nhất hay không? Nếu có, hãy xác định hệ số a và b.
Lời giải:
Hàm số y = 2x + 3 là hàm số bậc nhất vì nó có dạng y = ax + b, trong đó a = 2 và b = 3.
Câu b: (Ví dụ về một câu b cụ thể, giả sử là vẽ đồ thị hàm số)
Vẽ đồ thị hàm số y = -x + 1.
Lời giải:
Để vẽ đồ thị hàm số y = -x + 1, ta thực hiện các bước sau:
Bảng giá trị:
| x | y |
|---|---|
| 0 | 1 |
| 1 | 0 |
| -1 | 2 |
Câu c: (Ví dụ về một câu c cụ thể, giả sử là tìm giao điểm)
Tìm giao điểm của hai đường thẳng y = x + 2 và y = -x + 4.
Lời giải:
Để tìm giao điểm của hai đường thẳng y = x + 2 và y = -x + 4, ta giải hệ phương trình sau:
{ y = x + 2 y = -x + 4 }
Thay y = x + 2 vào phương trình y = -x + 4, ta được:
x + 2 = -x + 4
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 2, ta được:
y = 1 + 2 = 3
Vậy giao điểm của hai đường thẳng y = x + 2 và y = -x + 4 là (1; 3).
Để giải tốt các bài tập về hàm số bậc nhất, các em cần nắm vững các kiến thức cơ bản và luyện tập thường xuyên. Dưới đây là một số mẹo nhỏ có thể giúp các em:
Các em có thể tham khảo thêm các tài liệu sau để học tốt hơn về hàm số bậc nhất:
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải bài 5 trang 131 Vở thực hành Toán 9 tập 2. Chúc các em học tập tốt!