Chào mừng các em học sinh đến với lời giải chi tiết bài 4 trang 80 Vở thực hành Toán 9 tập 2. Bài học này thuộc chương trình đại số lớp 9, tập trung vào việc giải các bài toán liên quan đến hàm số bậc nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và các phương pháp giải toán hiệu quả.
Một công ty cần tuyển 2 nhân viên. Có 5 người nộp hồ sơ xin việc trong đó có 3 nam và 2 nữ. Vì khả năng của 5 người này là như nhau nên công ty chọn ngẫu nhiên lần lượt hai người. Tính xác suất để một nam, một nữ được chọn.
Đề bài
Một công ty cần tuyển 2 nhân viên. Có 5 người nộp hồ sơ xin việc trong đó có 3 nam và 2 nữ. Vì khả năng của 5 người này là như nhau nên công ty chọn ngẫu nhiên lần lượt hai người. Tính xác suất để một nam, một nữ được chọn.
Phương pháp giải - Xem chi tiết
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Lời giải chi tiết
Kí hiệu ba nam là A, B, C và hai nữ là D, E. Mỗi kết quả có thể cặp (X, Y) trong đó X, Y tương ứng là tên của ứng viên được chọn lần đầu và lần thứ hai với \(X \ne Y\).
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng sau:
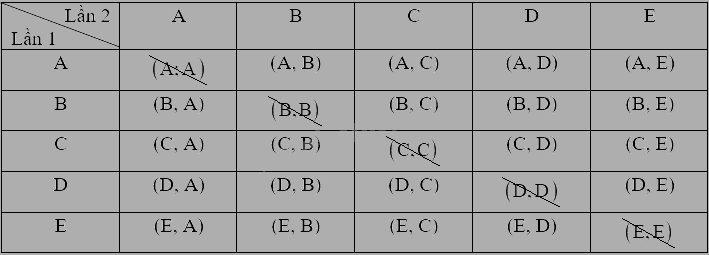
Vì \(X \ne Y\) nên cặp có hai phần tử trùng nhau không được tính, tức là trong bảng ta phải xóa 5 ô: (A, A); (B, B); (C, C); (D, D); (E, E). Vậy có 20 kết quả có thể là đồng khả năng.
Có kết quả thuận lợi cho biến cố “chọn được một nam, một nữ” là (A, D), (A, E), (B, D), (B, E), (C, D), (C, E), (D, A), (E, A), (D, B), (E, B), (D, C), (E, C).
Vậy xác suất cần tìm là \(\frac{{12}}{{20}} = \frac{3}{5}\).
Bài 4 trang 80 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng trong chương trình học Toán 9, giúp học sinh củng cố kiến thức về hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đồ thị hàm số và các phương pháp giải toán liên quan.
Bài 4 trang 80 Vở thực hành Toán 9 tập 2 thường bao gồm các dạng bài tập sau:
Để giải bài tập bài 4 trang 80 Vở thực hành Toán 9 tập 2, học sinh có thể áp dụng các phương pháp sau:
Dưới đây là lời giải chi tiết cho từng phần của bài 4 trang 80 Vở thực hành Toán 9 tập 2:
Đề bài: Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải:
Hệ số góc của hàm số y = 2x - 3 là a = 2.
Tung độ gốc của hàm số y = 2x - 3 là b = -3.
Đề bài: Vẽ đồ thị của hàm số y = 2x - 3.
Lời giải:
Để vẽ đồ thị của hàm số y = 2x - 3, ta chọn hai điểm thuộc đồ thị hàm số:
Nối hai điểm A(0; -3) và B(1; -1) lại, ta được đồ thị của hàm số y = 2x - 3.
Đề bài: Cho hàm số y = -x + 1. Tìm tọa độ giao điểm của hai đường thẳng y = 2x - 3 và y = -x + 1.
Lời giải:
Để tìm tọa độ giao điểm của hai đường thẳng y = 2x - 3 và y = -x + 1, ta giải hệ phương trình sau:
| y = 2x - 3 | y = -x + 1 | |
|---|---|---|
| Phương trình 1 | y = 2x - 3 | |
| Phương trình 2 | y = -x + 1 |
Thay y = -x + 1 vào phương trình y = 2x - 3, ta được:
-x + 1 = 2x - 3
3x = 4
x = 4/3
Thay x = 4/3 vào phương trình y = -x + 1, ta được:
y = -4/3 + 1 = -1/3
Vậy tọa độ giao điểm của hai đường thẳng y = 2x - 3 và y = -x + 1 là (4/3; -1/3).
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập tương tự sau:
Bài 4 trang 80 Vở thực hành Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày ở trên, các em sẽ tự tin hơn trong quá trình học tập.