Chào mừng các em học sinh đến với lời giải chi tiết bài 8 trang 35 Vở thực hành Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, giúp các em học tập tốt hơn và đạt kết quả cao trong môn Toán.
Trên một khu vườn hình vuông có cạnh bằng 20m người ta làm một lối đi xung quanh vườn có bề rộng x(m) (Hình dưới). Để diện tích lối đi là (76{m^2}) thì bề rộng x là bao nhiêu?
Đề bài
Trên một khu vườn hình vuông có cạnh bằng 20m người ta làm một lối đi xung quanh vườn có bề rộng x(m) (Hình dưới). Để diện tích lối đi là \(76{m^2}\) thì bề rộng x là bao nhiêu?
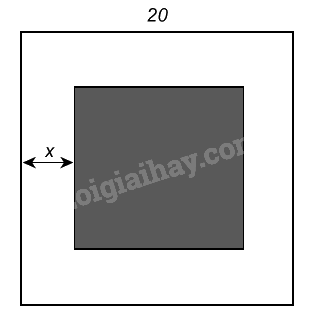
Phương pháp giải - Xem chi tiết
+ Dựa vào dữ kiện đầu bài, lập được phương trình có dạng phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
+ Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\). Sau đó lấy tất cả các nghiệm của chúng.
Lời giải chi tiết
Phần đất làm vườn là hình vuông có cạnh \(20 - x\left( m \right)\) và có diện tích đất là \({\left( {20 - x} \right)^2}\;\left( {{m^2}} \right)\)
Theo giả thiết, diện tích đất dành cho làm vườn là: \({20^2} - 76 = 324\left( {{m^2}} \right)\)
suy ra \({\left( {20 - x} \right)^2} = 324\) hay \({\left( {20 - x} \right)^2} = {18^2}\)
\({\left( {20 - x} \right)^2} - {18^2} = 0\)
\(\left( {20 - x - 18} \right)\left( {20 - x + 18} \right) = 0\)
\(\left( {2 - x} \right)\left( {38 - x} \right) = 0\)
Suy ra \(2 - x = 0\) hoặc \(38 - x = 0\)
+) \(2 - x = 0\) hay \( - x = - 2\), suy ra \(x = 2\)
+) \(38 - x = 0\) hay \( - x = - 38\), suy ra \(x = 38\) (loại vì bề rộng của lối đi phải bé hơn cạnh khu vườn)
Vậy bề rộng của lối đi là 2m.
Bài 8 trang 35 Vở thực hành Toán 9 thường thuộc chương trình học về hàm số bậc nhất. Đây là một phần quan trọng trong chương trình Toán lớp 9, giúp học sinh hiểu rõ hơn về các khái niệm cơ bản của hàm số và ứng dụng của chúng trong giải quyết các bài toán thực tế.
Bài 8 thường tập trung vào việc xác định hệ số góc của đường thẳng, viết phương trình đường thẳng khi biết hệ số góc và một điểm thuộc đường thẳng, hoặc khi biết hai điểm thuộc đường thẳng. Ngoài ra, bài tập còn yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán liên quan đến thực tế.
Để giải bài 8 trang 35 Vở thực hành Toán 9 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Bài toán: Viết phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc m = 3.
Giải:
Phương trình đường thẳng có dạng y = mx + b. Thay m = 3 và điểm A(1; 2) vào phương trình, ta có:
2 = 3 * 1 + b
=> b = -1
Vậy phương trình đường thẳng cần tìm là y = 3x - 1.
Để củng cố kiến thức về bài 8 trang 35 Vở thực hành Toán 9, các em có thể tự giải thêm các bài tập sau:
Bài 8 trang 35 Vở thực hành Toán 9 là một bài tập quan trọng, giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của chúng. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!