Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm trong Vở thực hành Toán 9. Chúng tôi hiểu rằng việc tự học Toán 9 đôi khi gặp nhiều khó khăn, đặc biệt là với các dạng bài tập trắc nghiệm đòi hỏi sự nhanh nhạy và chính xác.
Với mục tiêu hỗ trợ học sinh học Toán 9 hiệu quả, chúng tôi đã biên soạn và cung cấp bộ giải đáp đầy đủ cho các câu hỏi trắc nghiệm trang 5, 6 Vở thực hành Toán 9.
Phương trình nào sau đây là phương trình bậc nhất hai ẩn? A. ({x^2} - y = 2). B. (2x + y = 0). C. (0x - 0y = - 2). D. ({x^2} + {y^2} = 5).
Trả lời Câu 2 trang 6 Vở thực hành Toán 9
Nghiệm (tổng quát) của phương trình \( - 2x - 3y = 6\) là
A. \(\left( {x;\frac{2}{3}x + 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
B. \(\left( {\frac{3}{2}y + 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
C. \(\left( {\frac{3}{2}y - 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
D. \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Phương pháp giải:
Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.
Lời giải chi tiết:
Ta có: \( - 2x - 3y = 6\), suy ra \(y = \frac{{ - 2}}{3}x - 2\).
Do đó, nghiệm tổng quát của phương trình \( - 2x - 3y = 6\) là \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Chọn D
Trả lời Câu 3 trang 6 Vở thực hành Toán 9
Cho hai phương trình \( - 3x + y = - 7\;\left( 1 \right)\) và \(x - 2y = 4\;\left( 2 \right)\). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
A. \(\left( {0; - 7} \right)\).
B. \(\left( {6;1} \right)\).
C. \(\left( {2; - 1} \right)\).
D. \(\left( { - 1; - 10} \right)\).
Phương pháp giải:
Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).
Lời giải chi tiết:
Với \(x = 2;y = - 1\) ta có:
\( - 3.2 + \left( { - 1} \right) = - 7\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (1).
\(2 - 2\left( { - 1} \right) = 4\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (2).
Do đó, \(\left( {2; - 1} \right)\) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).
Chọn C
Trả lời Câu 1 trang 5 Vở thực hành Toán 9
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A. \({x^2} - y = 2\).
B. \(2x + y = 0\).
C. \(0x - 0y = - 2\).
D. \({x^2} + {y^2} = 5\).
Phương pháp giải:
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b, c, là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).
Lời giải chi tiết:
Phương trình \(2x + y = 0\) là phương trình bậc nhất hai ẩn.
Chọn B
Trả lời Câu 4 trang 6 Vở thực hành Toán 9
Hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn nào sau đây? trong đầu bài nó ghi là pt 1 ẩn, nhưng đúng là pt hai ẩn nên t sửa đề cho đúng luôn nhé
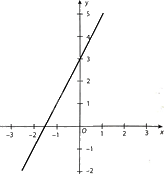
A. \(2x - y = - 3\).
B. \(2x + y = 3\).
C. \(3x + y = 3\).
D. \(3x - y = 0\).
Phương pháp giải:
Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn \(ax + by = c\) là một đường thẳng. Đường thẳng đó gọi là đường thẳng \(ax + by = c\).
Lời giải chi tiết:
Ta thấy, các điểm (0; 3) và \(\left( {\frac{{ - 3}}{2};0} \right)\) thuộc đường thẳng cần tìm.
Do đó, đường thẳng cần tìm là: \(2x - y = - 3\).
Vậy hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn \(2x - y = - 3\).
Chọn A
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 5 Vở thực hành Toán 9
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A. \({x^2} - y = 2\).
B. \(2x + y = 0\).
C. \(0x - 0y = - 2\).
D. \({x^2} + {y^2} = 5\).
Phương pháp giải:
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b, c, là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).
Lời giải chi tiết:
Phương trình \(2x + y = 0\) là phương trình bậc nhất hai ẩn.
Chọn B
Trả lời Câu 2 trang 6 Vở thực hành Toán 9
Nghiệm (tổng quát) của phương trình \( - 2x - 3y = 6\) là
A. \(\left( {x;\frac{2}{3}x + 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
B. \(\left( {\frac{3}{2}y + 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
C. \(\left( {\frac{3}{2}y - 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
D. \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Phương pháp giải:
Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.
Lời giải chi tiết:
Ta có: \( - 2x - 3y = 6\), suy ra \(y = \frac{{ - 2}}{3}x - 2\).
Do đó, nghiệm tổng quát của phương trình \( - 2x - 3y = 6\) là \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Chọn D
Trả lời Câu 3 trang 6 Vở thực hành Toán 9
Cho hai phương trình \( - 3x + y = - 7\;\left( 1 \right)\) và \(x - 2y = 4\;\left( 2 \right)\). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?
A. \(\left( {0; - 7} \right)\).
B. \(\left( {6;1} \right)\).
C. \(\left( {2; - 1} \right)\).
D. \(\left( { - 1; - 10} \right)\).
Phương pháp giải:
Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).
Lời giải chi tiết:
Với \(x = 2;y = - 1\) ta có:
\( - 3.2 + \left( { - 1} \right) = - 7\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (1).
\(2 - 2\left( { - 1} \right) = 4\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (2).
Do đó, \(\left( {2; - 1} \right)\) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).
Chọn C
Trả lời Câu 4 trang 6 Vở thực hành Toán 9
Hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn nào sau đây? trong đầu bài nó ghi là pt 1 ẩn, nhưng đúng là pt hai ẩn nên t sửa đề cho đúng luôn nhé
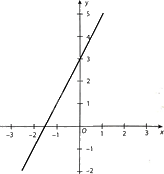
A. \(2x - y = - 3\).
B. \(2x + y = 3\).
C. \(3x + y = 3\).
D. \(3x - y = 0\).
Phương pháp giải:
Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn \(ax + by = c\) là một đường thẳng. Đường thẳng đó gọi là đường thẳng \(ax + by = c\).
Lời giải chi tiết:
Ta thấy, các điểm (0; 3) và \(\left( {\frac{{ - 3}}{2};0} \right)\) thuộc đường thẳng cần tìm.
Do đó, đường thẳng cần tìm là: \(2x - y = - 3\).
Vậy hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn \(2x - y = - 3\).
Chọn A
Bài tập trắc nghiệm trong Vở thực hành Toán 9 trang 5 và 6 thường tập trung vào các kiến thức cơ bản về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong thực tế. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững định nghĩa, tính chất của hàm số, và các phương pháp xác định hệ số góc.
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Hệ số góc a quyết định độ dốc của đường thẳng biểu diễn hàm số. Nếu a > 0, hàm số đồng biến; nếu a < 0, hàm số nghịch biến; nếu a = 0, hàm số là hàm hằng.
Để giải bài tập trắc nghiệm nhanh và chính xác, học sinh nên áp dụng các phương pháp sau:
Dưới đây là giải chi tiết một số câu hỏi trắc nghiệm tiêu biểu:
Đáp án: a = 2
Giải thích: Hàm số y = ax + b có hệ số góc là a. Trong trường hợp này, a = 2.
Đáp án: y = -x + 3
Giải thích: Sử dụng công thức phương trình đường thẳng đi qua điểm A(x0; y0) và có hệ số góc a: y - y0 = a(x - x0). Thay x0 = 1, y0 = 2, a = -1 vào công thức, ta được y - 2 = -1(x - 1) => y = -x + 3.
Đáp án: (1; 2)
Giải thích: Giải hệ phương trình:
y = x + 1
y = -x + 3
Thay y = x + 1 vào phương trình thứ hai, ta được x + 1 = -x + 3 => 2x = 2 => x = 1. Thay x = 1 vào phương trình y = x + 1, ta được y = 2. Vậy giao điểm là (1; 2).
Để nắm vững kiến thức về hàm số bậc nhất và các ứng dụng của nó, học sinh nên luyện tập thêm các bài tập trong sách giáo khoa, sách bài tập, và các đề thi thử. Ngoài ra, việc tham gia các khóa học trực tuyến hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè cũng rất hữu ích.
Việc giải các câu hỏi trắc nghiệm trang 5, 6 Vở thực hành Toán 9 là một bước quan trọng trong quá trình học Toán 9. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải hiệu quả, và luyện tập thường xuyên, học sinh có thể tự tin đối mặt với các bài kiểm tra và thi cử.