Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 74 Vở thực hành Toán 9. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Cho tam giác vuông có một góc nhọn ({30^o}) và cạnh đối với góc này bằng 5cm. Tính độ dài cạnh huyền của tam giác
Đề bài
Cho tam giác vuông có một góc nhọn \({30^o}\) và cạnh đối với góc này bằng 5cm. Tính độ dài cạnh huyền của tam giác
Phương pháp giải - Xem chi tiết
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \). Ta có tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
Lời giải chi tiết
(H.4.7)
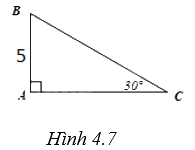
Xét tam giác ABC vuông tại A, có \(AB = 5\), \(\widehat C = {30^o}\). Ta cần tính cạnh BC.
Trong tam giác ABC vuông, ta có \(\sin C = \frac{{AB}}{{BC}}\), hay \(\sin {30^o} = \frac{{AB}}{{BC}}\), suy ra \(\frac{1}{2} = \frac{5}{{BC}}\), hay\(BC = 5:\frac{1}{2} = 10\left( {cm} \right)\)
Bài 3 trang 74 Vở thực hành Toán 9 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị hàm số, và giải các phương trình, bất phương trình liên quan.
Bài 3 thường bao gồm các dạng bài tập sau:
Để xác định hàm số, ta cần sử dụng các thông tin đã cho để tìm các hệ số của hàm số. Ví dụ, nếu biết đồ thị đi qua hai điểm A(x1, y1) và B(x2, y2), ta có thể thay tọa độ của hai điểm này vào phương trình hàm số để tìm các hệ số.
Hệ số góc của đường thẳng biểu diễn hàm số y = ax + b là a. Để tìm hệ số góc, ta có thể sử dụng công thức tính độ dốc của đường thẳng hoặc dựa vào phương trình hàm số.
Để kiểm tra xem một điểm M(x0, y0) có thuộc đồ thị của hàm số y = f(x) hay không, ta thay x0 vào hàm số và tính y. Nếu y = y0, thì điểm M thuộc đồ thị của hàm số.
Để giải phương trình hoặc bất phương trình liên quan đến hàm số, ta cần sử dụng các kiến thức về giải phương trình, bất phương trình bậc nhất và bậc hai. Đồng thời, ta cũng cần chú ý đến điều kiện xác định của hàm số.
Trong các bài toán ứng dụng thực tế, ta cần phân tích đề bài để xác định các yếu tố liên quan đến hàm số, sau đó xây dựng phương trình hoặc bất phương trình để giải quyết bài toán.
Ví dụ: Cho hàm số y = 2x - 1. Hãy xác định xem điểm A(1, 1) có thuộc đồ thị của hàm số hay không.
Giải: Thay x = 1 vào hàm số, ta được y = 2(1) - 1 = 1. Vì y = 1, nên điểm A(1, 1) thuộc đồ thị của hàm số y = 2x - 1.
Ngoài Vở thực hành Toán 9, các em có thể tham khảo thêm sách giáo khoa Toán 9, các bài giảng trực tuyến, và các trang web học Toán uy tín để nắm vững kiến thức và kỹ năng giải bài tập.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài 3 trang 74 Vở thực hành Toán 9 một cách hiệu quả. Chúc các em học tập tốt!