Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 9. Chúng tôi hiểu rằng việc giải các bài tập trắc nghiệm trong Vở thực hành Toán 9 có thể gặp nhiều khó khăn.
Do đó, chúng tôi đã biên soạn bộ giải đáp đầy đủ, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong Hình 4.35, (cos alpha ) bằng A. (frac{5}{3}). B. (frac{3}{4}). C. (frac{3}{5}). D. (frac{4}{5}).
Trả lời Câu 4 trang 90 Vở thực hành Toán 9
Với mọi góc nhọn \(\alpha \), ta có
A. \(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
B. \(\tan \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
C. \(\cot \left( {{{90}^o} - \alpha } \right) = 1 - \tan \alpha \).
D. \(\cot \left( {{{90}^o} - \alpha } \right) = \sin \alpha \).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
\(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \)
Chọn A
Trả lời Câu 5 trang 90 Vở thực hành Toán 9
Giá trị \(\tan {30^o}\) bằng
A. \(\sqrt 3 \).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 1.
Phương pháp giải:
\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)
Lời giải chi tiết:
\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)
Chọn C
Trả lời Câu 1 trang 90 Vở thực hành Toán 9
Trong Hình 4.35, \(\cos \alpha \) bằng
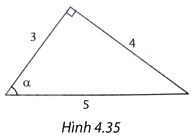
A. \(\frac{5}{3}\).
B. \(\frac{3}{4}\).
C. \(\frac{3}{5}\).
D. \(\frac{4}{5}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
Lời giải chi tiết:
\(\cos \alpha = \frac{3}{5}\)
Chọn C
Trả lời Câu 2 trang 90 Vở thực hành Toán 9
Trong tam giác MNP vuông tại M (H.4.36), \(\sin \widehat {MNP}\) bằng
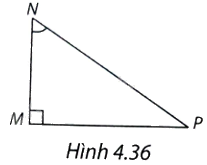
A. \(\frac{{PN}}{{NM}}\).
B. \(\frac{{MP}}{{PN}}\).
C. \(\frac{{MN}}{{PN}}\).
D. \(\frac{{MN}}{{MP}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
Lời giải chi tiết:
\(\sin \widehat {MNP} = \frac{{MP}}{{PN}}\)
Chọn B
Trả lời Câu 6 trang 90 Vở thực hành Toán 9
Cho tam giác MNP như Hình 4.38, MH là đường cao, \(\widehat {MPN} = {60^o},MN = 2\sqrt 3 \). Khi đó
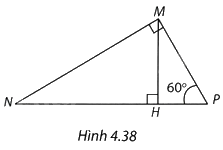
A. \(MP = \frac{1}{2}\).
B. \(\widehat {MNP} = {45^o}\).
C. \(MP = \frac{1}{3}\).
D. \(\widehat {MNP} = {30^o}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
Tam giác MNP vuông tại M nên
\(\widehat {MNP} = {90^o} - \widehat P = {30^o}\),
\(MP = MN.\cot {60^o} = 2\sqrt 3 .\frac{1}{{\sqrt 3 }} = 2\)
Chọn D
Trả lời Câu 3 trang 90 Vở thực hành Toán 9
Trong tam giác ABC vuông tại A (H.4.37), tanB bằng
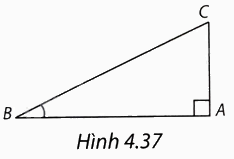
A. \(\frac{{AB}}{{AC}}\).
B. \(\frac{{AC}}{{AB}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{BC}}{{AC}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
Lời giải chi tiết:
Vì tam giác ABC vuông tại A nên \(tanB = \frac{{AC}}{{AB}}\)
Chọn B
Chọn phương án đúng trong mỗi câu sau:
Trả lời Câu 1 trang 90 Vở thực hành Toán 9
Trong Hình 4.35, \(\cos \alpha \) bằng
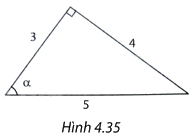
A. \(\frac{5}{3}\).
B. \(\frac{3}{4}\).
C. \(\frac{3}{5}\).
D. \(\frac{4}{5}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
Lời giải chi tiết:
\(\cos \alpha = \frac{3}{5}\)
Chọn C
Trả lời Câu 2 trang 90 Vở thực hành Toán 9
Trong tam giác MNP vuông tại M (H.4.36), \(\sin \widehat {MNP}\) bằng
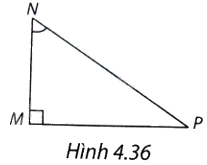
A. \(\frac{{PN}}{{NM}}\).
B. \(\frac{{MP}}{{PN}}\).
C. \(\frac{{MN}}{{PN}}\).
D. \(\frac{{MN}}{{MP}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh huyền gọi là sin của \(\alpha \).
Lời giải chi tiết:
\(\sin \widehat {MNP} = \frac{{MP}}{{PN}}\)
Chọn B
Trả lời Câu 3 trang 90 Vở thực hành Toán 9
Trong tam giác ABC vuông tại A (H.4.37), tanB bằng
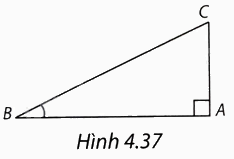
A. \(\frac{{AB}}{{AC}}\).
B. \(\frac{{AC}}{{AB}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{BC}}{{AC}}\).
Phương pháp giải:
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh đối và cạnh kề gọi là tan của \(\alpha \).
Lời giải chi tiết:
Vì tam giác ABC vuông tại A nên \(tanB = \frac{{AC}}{{AB}}\)
Chọn B
Trả lời Câu 4 trang 90 Vở thực hành Toán 9
Với mọi góc nhọn \(\alpha \), ta có
A. \(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
B. \(\tan \left( {{{90}^o} - \alpha } \right) = \cos \alpha \).
C. \(\cot \left( {{{90}^o} - \alpha } \right) = 1 - \tan \alpha \).
D. \(\cot \left( {{{90}^o} - \alpha } \right) = \sin \alpha \).
Phương pháp giải:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Lời giải chi tiết:
\(\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \)
Chọn A
Trả lời Câu 5 trang 90 Vở thực hành Toán 9
Giá trị \(\tan {30^o}\) bằng
A. \(\sqrt 3 \).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 1.
Phương pháp giải:
\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)
Lời giải chi tiết:
\(\tan {30^o} = \frac{1}{{\sqrt 3 }}\)
Chọn C
Trả lời Câu 6 trang 90 Vở thực hành Toán 9
Cho tam giác MNP như Hình 4.38, MH là đường cao, \(\widehat {MPN} = {60^o},MN = 2\sqrt 3 \). Khi đó
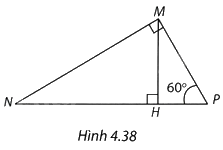
A. \(MP = \frac{1}{2}\).
B. \(\widehat {MNP} = {45^o}\).
C. \(MP = \frac{1}{3}\).
D. \(\widehat {MNP} = {30^o}\).
Phương pháp giải:
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.
Lời giải chi tiết:
Tam giác MNP vuông tại M nên
\(\widehat {MNP} = {90^o} - \widehat P = {30^o}\),
\(MP = MN.\cot {60^o} = 2\sqrt 3 .\frac{1}{{\sqrt 3 }} = 2\)
Chọn D
Trang 90 Vở thực hành Toán 9 thường chứa các bài tập trắc nghiệm liên quan đến các chủ đề quan trọng như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, và các ứng dụng thực tế của đại số. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập là điều cần thiết để đạt kết quả tốt trong môn Toán.
Các câu hỏi trắc nghiệm trên trang 90 thường tập trung vào việc kiểm tra khả năng:
Dưới đây là giải chi tiết một số câu hỏi trắc nghiệm thường gặp trên trang 90 Vở thực hành Toán 9:
Giải: Thay x = -1 vào hàm số y = 2x + 3, ta được: y = 2*(-1) + 3 = -2 + 3 = 1. Vậy, giá trị của y khi x = -1 là 1.
Giải: Cộng hai phương trình lại, ta được: 3x = 6 => x = 2. Thay x = 2 vào phương trình x - y = 1, ta được: 2 - y = 1 => y = 1. Vậy, hệ phương trình có nghiệm duy nhất (x, y) = (2, 1).
Giải: Quãng đường đi được là: S = v * t = 40 * 2 = 80 km. Vậy, sau 2 giờ người đó đi được 80 km.
Để giải nhanh các bài tập trắc nghiệm Toán 9, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm các bài tập tương tự trong sách giáo khoa, sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi làm bài kiểm tra.
Ngoài Vở thực hành Toán 9, bạn có thể tham khảo thêm các tài liệu sau:
Việc giải các câu hỏi trắc nghiệm trang 90 Vở thực hành Toán 9 đòi hỏi sự nắm vững kiến thức, kỹ năng và phương pháp giải bài tập. Hy vọng với hướng dẫn chi tiết và các mẹo giải nhanh trên đây, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt trong môn Toán.
Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích và lời giải bài tập Toán 9.