Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều. Bài viết này được thiết kế để giúp các em hiểu rõ phương pháp giải bài tập, nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 tập 1 đầy đủ, chính xác, được trình bày một cách dễ hiểu, phù hợp với trình độ của học sinh.
Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc
Đề bài
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Phương pháp giải - Xem chi tiết
Dựa vào các giá trị lượng giác để tính từng cạnh của tam giác MNP
Lời giải chi tiết
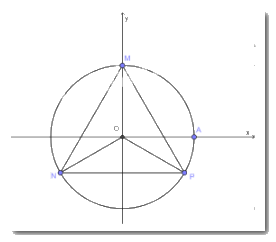
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều thuộc chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về điều kiện xác định của hàm số để tìm tập xác định của các hàm số được cho.
Bài 1 gồm các hàm số khác nhau, yêu cầu học sinh xác định tập xác định của từng hàm số. Các hàm số có thể bao gồm hàm số phân thức, hàm số chứa căn bậc hai, hàm số chứa logarit, và các hàm số kết hợp.
Để giải bài tập này, học sinh cần nắm vững các quy tắc sau:
a) y = √(2x - 1)
Điều kiện xác định: 2x - 1 ≥ 0 ⇔ 2x ≥ 1 ⇔ x ≥ 1/2
Vậy tập xác định của hàm số là D = [1/2; +∞)
b) y = 1 / (x - 3)
Điều kiện xác định: x - 3 ≠ 0 ⇔ x ≠ 3
Vậy tập xác định của hàm số là D = R \ {3}
c) y = log₂(x + 2)
Điều kiện xác định: x + 2 > 0 ⇔ x > -2
Vậy tập xác định của hàm số là D = (-2; +∞)
d) y = √(x² - 4)
Điều kiện xác định: x² - 4 ≥ 0 ⇔ x² ≥ 4 ⇔ |x| ≥ 2 ⇔ x ≤ -2 hoặc x ≥ 2
Vậy tập xác định của hàm số là D = (-∞; -2] ∪ [2; +∞)
Khi giải bài tập về tập xác định của hàm số, học sinh cần chú ý:
Để củng cố kiến thức, học sinh có thể tự giải các bài tập tương tự sau:
Bài 1 trang 15 SGK Toán 11 tập 1 - Cánh diều là bài tập cơ bản giúp học sinh làm quen với khái niệm tập xác định của hàm số. Việc nắm vững phương pháp giải bài tập này sẽ là nền tảng quan trọng cho việc học các kiến thức tiếp theo trong chương trình Toán 11.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn trong việc giải bài tập Toán 11 tập 1 - Cánh diều. Chúc các em học tập tốt!