Giải Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải pháp học toán hiệu quả

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.

Chúng tôi cam kết cung cấp nội dung chính xác, cập nhật và phù hợp với chương trình học Toán 11 hiện hành. Hãy cùng bắt đầu khám phá lời giải chi tiết cho bài tập này!

Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho (BI = 2IC). Chứng minh rằng IG song song với mặt phẳng (ACD).

Đề bài

Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho \(BI = 2IC\). Chứng minh rằng IG song song với mặt phẳng (ACD).

Phương pháp giải - Xem chi tiết Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều 1

Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) thì a song song với (P)

Lời giải chi tiết

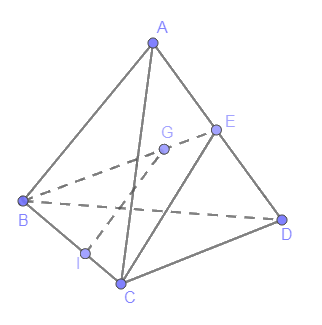
Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều 2

Tam giác BCE có E là trung điểm AD

Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)

Theo Ta lét, IG //CE

Mà CE thuộc (ACD)

Suy ra: IG // (ACD)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều: Giải chi tiết và hướng dẫn

Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều thuộc chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại một điểm và các tính chất của giới hạn để giải quyết các bài toán cụ thể.

Nội dung bài tập

Bài 3 thường bao gồm các dạng bài tập sau:

Tính giới hạn của hàm số tại một điểm bằng định nghĩa.
Tính giới hạn của hàm số sử dụng các tính chất của giới hạn.
Xác định xem một hàm số có giới hạn tại một điểm hay không.
Ứng dụng giới hạn để giải các bài toán thực tế.

Hướng dẫn giải chi tiết

Để giải quyết bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:

Định nghĩa giới hạn: Hiểu rõ định nghĩa giới hạn của hàm số tại một điểm.
Giới hạn một bên: Biết cách tính giới hạn bên trái và giới hạn bên phải của hàm số tại một điểm.
Tính chất của giới hạn: Vận dụng các tính chất của giới hạn để đơn giản hóa bài toán.
Các dạng giới hạn đặc biệt: Nhận biết và giải quyết các dạng giới hạn đặc biệt như giới hạn vô cùng.

Dưới đây là ví dụ minh họa cách giải một bài tập trong Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều:

Ví dụ minh họa

Bài tập: Tính lim_x→2 (x² - 4) / (x - 2)

Giải:

Ta có:

lim_x→2 (x² - 4) / (x - 2) = lim_x→2 (x - 2)(x + 2) / (x - 2)

= lim_x→2 (x + 2)

= 2 + 2 = 4

Vậy, lim_x→2 (x² - 4) / (x - 2) = 4

Lưu ý khi giải bài tập

Luôn kiểm tra xem hàm số có xác định tại điểm cần tính giới hạn hay không.
Sử dụng các tính chất của giới hạn một cách linh hoạt để đơn giản hóa bài toán.
Chú ý đến các dạng giới hạn đặc biệt và áp dụng các công thức phù hợp.
Kiểm tra lại kết quả sau khi giải bài tập.

Bài tập luyện tập

Để củng cố kiến thức và kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập sau:

Bài 1 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Bài 2 trang 104 SGK Toán 11 tập 1 - Cánh Diều
Bài 4 trang 104 SGK Toán 11 tập 1 - Cánh Diều

Kết luận

Bài 3 trang 104 SGK Toán 11 tập 1 - Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về khái niệm giới hạn của hàm số. Bằng cách nắm vững kiến thức lý thuyết và rèn luyện kỹ năng giải bài tập, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến giới hạn.

Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!