Bài học này cung cấp kiến thức nền tảng về hai mặt phẳng vuông góc trong chương trình Toán 11 Cánh diều. Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện để hai mặt phẳng vuông góc, và các tính chất quan trọng liên quan.
Nội dung được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể, giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Đây là bước đệm quan trọng để giải quyết các bài toán hình học không gian phức tạp hơn.
1. Định nghĩa Hai mặt phẳng cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là hai góc nhị diện vuông thì hai mặt phẳng đã cho gọi là vuông góc với nhau.
1. Định nghĩa
Hai mặt phẳng cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là hai góc nhị diện vuông thì hai mặt phẳng đã cho gọi là vuông góc với nhau.
Ví dụ: Hai mặt phẳng (P) và (Q) cắt nhau tạo nên bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì vta nói (P) vuông góc với (Q), kí hiệu là \(\left( P \right) \bot \left( Q \right)\) hoặc \(\left( Q \right) \bot \left( P \right)\).
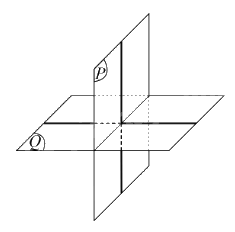
2. Điều kiện để hai mặt phẳng vuông góc
Nếu mặt phẳng này chứa một đường thẳng mà đường thẳng đó vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.
3. Tính chất
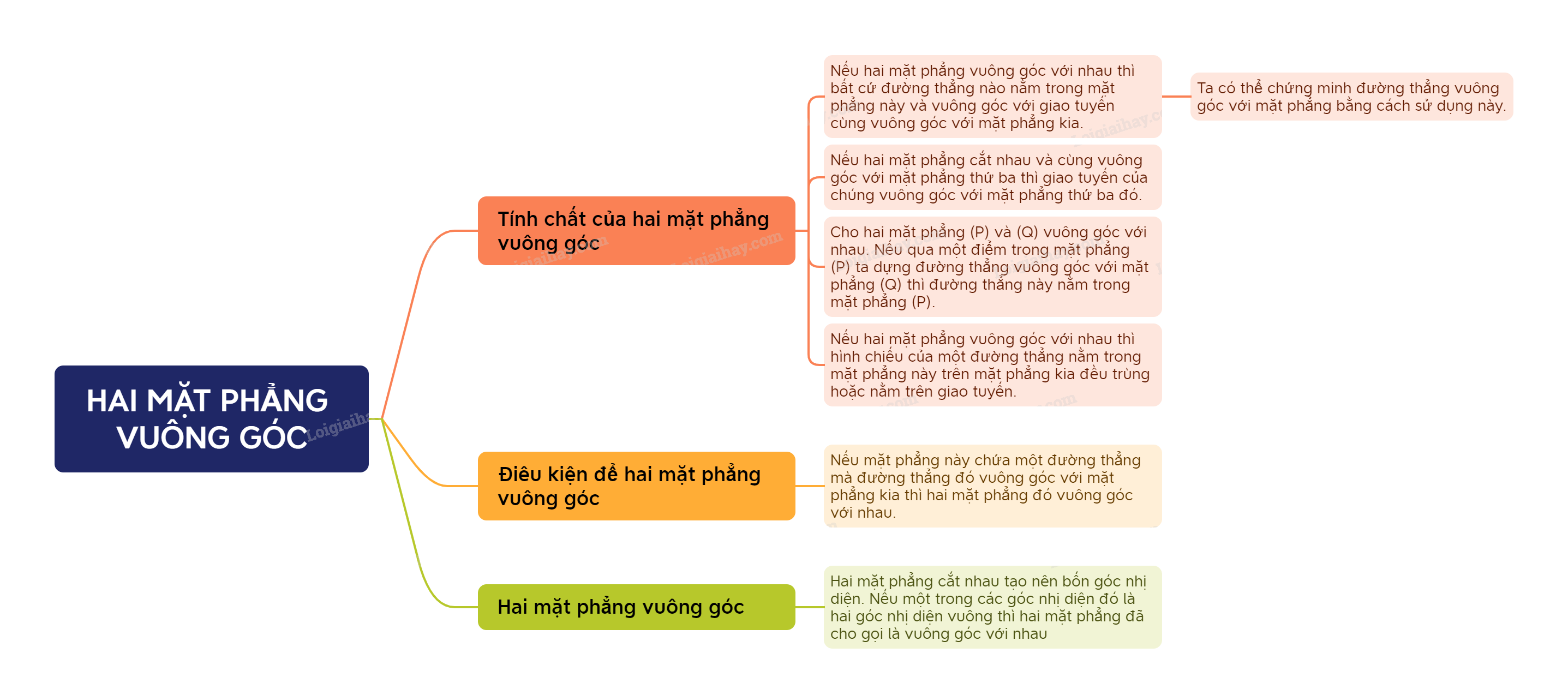
- Tính chất 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cùng vuông góc với mặt phẳng kia.
- Tính chất 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
Nhận xét:
- Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu qua một điểm trong mặt phẳng (P) ta dựng đường thẳng vuông góc với mặt phẳng (Q) thì đường thẳng này nằm trong mặt phẳng (P).
- Nếu hai mặt phẳng vuông góc với nhau thì hình chiếu của một đường thẳng nằm trong mặt phẳng này trên mặt phẳng kia đều trùng hoặc nằm trên giao tuyến.
- Ta có thể chứng minh đường thẳng vuông góc với mặt phẳng bằng cách sử dụng Tính chất 1.
Trong chương trình Hình học không gian lớp 11, kiến thức về hai mặt phẳng vuông góc đóng vai trò then chốt. Việc nắm vững lý thuyết này không chỉ giúp học sinh hiểu sâu sắc hơn về mối quan hệ giữa các mặt phẳng trong không gian mà còn là nền tảng để giải quyết các bài toán phức tạp liên quan.
Hai mặt phẳng được gọi là vuông góc nếu góc giữa chúng bằng 90°. Để xác định góc giữa hai mặt phẳng, ta thực hiện các bước sau:
Có một số điều kiện để xác định hai mặt phẳng vuông góc:
Khi hai mặt phẳng vuông góc, ta có những tính chất sau:
Lý thuyết hai mặt phẳng vuông góc được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến:
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi O là giao điểm của AC và BD. Biết SO vuông góc với mặt phẳng (ABCD). Chứng minh rằng (SAB) và (SAD) vuông góc với nhau.
Giải:
Vì SO vuông góc với (ABCD) nên SO vuông góc với AB và AD. Do đó, SO là đường cao của tam giác SAB và tam giác SAD. Xét tam giác SAB và tam giác SAD, ta có:
Vậy (SAB) ⊥ (SAD).
Để củng cố kiến thức, các bạn có thể tự giải các bài tập sau:
Lý thuyết hai mặt phẳng vuông góc là một phần quan trọng trong chương trình Hình học không gian lớp 11. Việc nắm vững lý thuyết và rèn luyện kỹ năng giải bài tập sẽ giúp học sinh tự tin hơn trong việc giải quyết các vấn đề liên quan đến không gian và hình học.