Chào mừng các em học sinh đến với lời giải chi tiết Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều. Bài học này thuộc chương trình học Toán 11 tập 1, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều một cách rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi ({G_1},{G_2}) lần lượt là trọng tâm của các tam giác ABC và ABD. Chứng minh rằng đường thẳng ({G_1}{G_2}) song song với đường thẳng CD.
Đề bài
Cho tứ diện ABCD. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm của các tam giác ABC và ABD. Chứng minh rằng đường thẳng \({G_1}{G_2}\) song song với đường thẳng CD.
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lời giải chi tiết
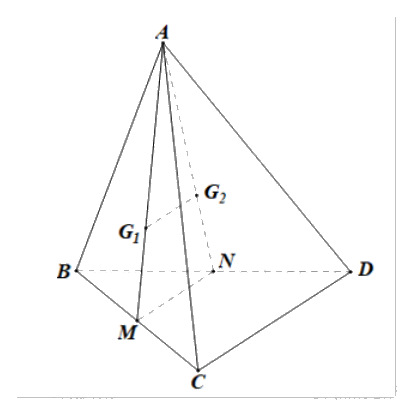
Trong mặt phẳng ABC, kẻ trung tuyến AM của tam giác ABC.
Vì \({G_1}\) là trọng tâm tam giác ABC nên \(\frac{{A{G_1}}}{{AM}} = \frac{2}{3}\).
Trong mặt phẳng ABD, kẻ trung tuyến AN của tam giác ABN.
Vì \({G_2}\) là trọng tâm tam giác ABC nên \(\frac{{A{G_2}}}{{AN}} = \frac{2}{3}\).
Xét tam giác AMN, có \(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}} = \frac{2}{3}\) nên \({G_1}{G_2}\)//MN (định lý Thales đảo).
Xét tam giác BCD có M, N lần lượt là trung điểm của BC, BD nên MN là đường trung bình.
Khi đó, MN//CD.
Vậy \({G_1}{G_2}\)//CD (cùng song song với MN).
Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai và các tính chất của parabol để giải quyết. Dưới đây là lời giải chi tiết và phân tích chuyên sâu về bài tập này:
Bài 4 yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Ví dụ: Xét hàm số y = 2x2 - 8x + 6.
Bước 1: Xác định các hệ số a, b, c.
a = 2, b = -8, c = 6.
Bước 2: Xác định đỉnh của parabol.
Δ = (-8)2 - 4 * 2 * 6 = 64 - 48 = 16.
xI = -(-8) / (2 * 2) = 2.
yI = -16 / (4 * 2) = -2.
Vậy đỉnh của parabol là I(2, -2).
Bước 3: Tìm trục đối xứng của parabol.
x = 2.
Bước 4: Vẽ đồ thị hàm số.
Đồ thị hàm số là một parabol có đỉnh I(2, -2) và trục đối xứng x = 2. Parabol mở lên trên vì a = 2 > 0.
Bước 5: Xác định khoảng đồng biến, nghịch biến của hàm số.
Hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).
Bước 6: Tìm giá trị nhỏ nhất của hàm số.
Giá trị nhỏ nhất của hàm số là -2 tại x = 2.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và phân tích chuyên sâu này, các em sẽ hiểu rõ hơn về Bài 4 trang 100 SGK Toán 11 tập 1 - Cánh diều và tự tin giải quyết các bài tập tương tự. Chúc các em học tốt!