Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều

Chào mừng bạn đến với bài học về Lý thuyết Đạo hàm cấp hai trong chương trình Toán 11 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn kiến thức nền tảng và các công thức quan trọng để hiểu và vận dụng đạo hàm cấp hai vào giải quyết các bài toán thực tế.

Chúng tôi cam kết mang đến cho bạn một trải nghiệm học tập trực tuyến hiệu quả, với nội dung được trình bày rõ ràng, dễ hiểu và có nhiều ví dụ minh họa.

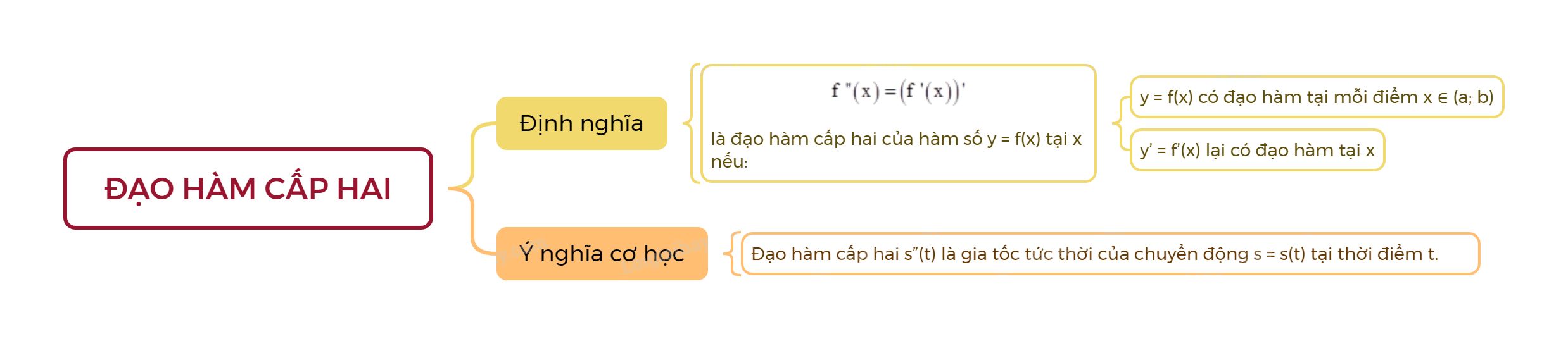
1. Định nghĩa

1. Định nghĩa

Giả sử hàm số y = f(x) có đạo hàm y’ = f’(x) tại mọi điểm \(x \in \left( {a;b} \right)\). Nếu hàm số y’ = f’(x) tiếp tục có đạo hàm tại x thì ta gọi đạo hàm của y’ tại x là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).

2. Ý nghĩa cơ học

Đạo hàm cấp hai s”(t) là gia tốc tức thời của chuyển động s = s(t) tại thời điểm t.

Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều 1

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều – hành trang không thể thiếu trong chuyên mục Ôn tập Toán lớp 11 trên nền tảng học toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Lý thuyết Đạo hàm cấp hai - Toán 11 Cánh diều

Đạo hàm cấp hai, hay đạo hàm bậc hai, là đạo hàm của đạo hàm cấp một của một hàm số. Nó cung cấp thông tin về tốc độ thay đổi của tốc độ thay đổi của hàm số, giúp chúng ta phân tích tính chất lồi lõm, điểm uốn và các đặc điểm quan trọng khác của đồ thị hàm số.

1. Định nghĩa Đạo hàm cấp hai

Cho hàm số y = f(x) có đạo hàm f'(x). Đạo hàm cấp hai của f(x), ký hiệu là f''(x), là đạo hàm của f'(x). Tức là:

f''(x) = (f'(x))'

Nếu f''(x) tồn tại tại một điểm x₀, ta nói hàm số f(x) có đạo hàm cấp hai tại x₀.

2. Công thức tính Đạo hàm cấp hai

Để tính đạo hàm cấp hai, ta thực hiện tuần tự các bước sau:

Tính đạo hàm cấp một f'(x).
Tính đạo hàm của f'(x) để được đạo hàm cấp hai f''(x).

Ví dụ:

Cho hàm số y = x³ + 2x² - x + 1

f'(x) = 3x² + 4x - 1

f''(x) = 6x + 4

3. Ý nghĩa của Đạo hàm cấp hai

Đạo hàm cấp hai có nhiều ứng dụng quan trọng trong việc phân tích hàm số:

Tính lồi lõm của hàm số:
- Nếu f''(x) > 0 trên một khoảng, hàm số f(x) lồi trên khoảng đó.
- Nếu f''(x) < 0 trên một khoảng, hàm số f(x) lõm trên khoảng đó.
Điểm uốn: Điểm uốn là điểm mà tại đó hàm số đổi từ lồi sang lõm hoặc ngược lại. Tại điểm uốn, đạo hàm cấp hai bằng 0 hoặc không tồn tại.
Ứng dụng trong các bài toán tối ưu: Đạo hàm cấp hai giúp xác định cực đại, cực tiểu của hàm số.

4. Ví dụ minh họa

Xét hàm số y = x⁴ - 2x² + 1

f'(x) = 4x³ - 4x

f''(x) = 12x² - 4

Để tìm điểm uốn, ta giải phương trình f''(x) = 0:

12x² - 4 = 0 => x² = 1/3 => x = ±√(1/3)

Vậy hàm số có hai điểm uốn tại x = √(1/3) và x = -√(1/3).

5. Bài tập áp dụng

Hãy tính đạo hàm cấp hai của các hàm số sau:

y = sin(2x)
y = e^x + ln(x)
y = x⁵ - 3x³ + 2

6. Kết luận

Lý thuyết Đạo hàm cấp hai là một phần quan trọng trong chương trình Toán 11 Cánh diều. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán liên quan đến tính chất của hàm số và ứng dụng trong thực tế. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.