Bài 3 trang 79 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Cánh Diều, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 3 trang 79, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và (widehat {SAB} = 100^circ ) (Hình 8) .
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = 100^\circ \) (Hình 8) . Tính góc giữa hai đường thẳng:
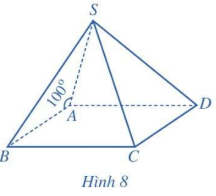
a) SA và AB
b) SA và CD
Phương pháp giải - Xem chi tiết
Dựa vào các xác định góc giữa hai đường thẳng đã học để làm
Lời giải chi tiết
Cách giải:
a) Vì \( \widehat {SAB} = 100^\circ \) nên
\(\left( {SA,AB} \right) = 180^0 - \widehat {SAB} = 180^0 - 100^\circ = 80^0 \)
Vậy góc giữa hai đường thẳng SA và AB bằng \( 80^0 \)
b) Do ABCD là hình bình hành => AB // CD
\( \Rightarrow \left( {SA, CD} \right) = \left( {SA, AB} \right) = 80^\circ \)
Vậy góc giữa hai đường thẳng SA và CD bằng \( 80^0 \)
Bài 3 trang 79 SGK Toán 11 tập 2 - Cánh Diều yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tốc độ thay đổi của đại lượng. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức đạo hàm cơ bản, cũng như kỹ năng phân tích và giải quyết vấn đề.
Bài tập thường xoay quanh các tình huống thực tế, ví dụ như tính vận tốc của một vật chuyển động, tính tốc độ thay đổi của sản lượng, hoặc tính độ dốc của một đường cong. Để giải quyết các bài toán này, học sinh cần:
Ví dụ: Một vật chuyển động theo phương trình s(t) = t2 + 2t + 1 (trong đó s là quãng đường, t là thời gian). Tính vận tốc của vật tại thời điểm t = 3.
Giải:
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải quyết Bài 3 trang 79 SGK Toán 11 tập 2 - Cánh Diều một cách hiệu quả. Chúc các bạn học tập tốt!