Bài 3 trang 25 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Cánh Diều, tập trung vào việc vận dụng kiến thức về hàm số và đồ thị để giải các bài toán thực tế. Bài học này giúp học sinh củng cố kiến thức đã học và rèn luyện kỹ năng giải bài tập.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 3 trang 25 SGK Toán 11 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilomet) của 40 chiếc ô tô:
Đề bài
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilomet) của 40 chiếc ô tô:

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng: [100 ; 120), [120 ; 140), [140 ; 160), [160 ; 180), [180 ; 200)
b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.
c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Lần lượt đếm số lượng của từng nhóm để lập bảng
- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
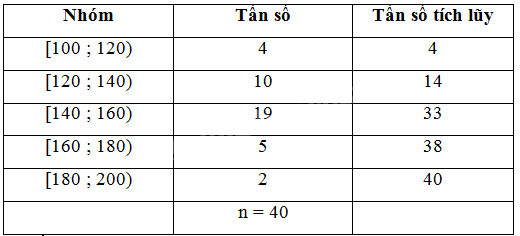
a) Các đại lượng tiêu biểu:
- Trung bình cộng: \(\overline x = \frac{{110.4 + 130.10 + 150.19 + 170.5 + 190.2}}{{40}} = 145,5\)
- Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 140 + \left( {\frac{{20 - 14}}{{19}}} \right).20 = \frac{{2780}}{{19}}\)
- Tứ phân vị:
+ Tứ phân vị thứ hai \({Q_2} = {M_e} = \frac{{2780}}{{19}}\)
+ Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 120 + \left( {\frac{{10 - 4}}{{10}}} \right).20 = 132\)
+ Tứ phân vị thứ ba: \(Q = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 140 + \left( {\frac{{30 - 14}}{{19}}} \right).20 = \frac{{2980}}{{19}}\)
b) Mốt của mẫu số liệu:\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 140 + \left( {\frac{{19 - 10}}{{2.19 - 10 - 5}}} \right).20 = \frac{{3400}}{{23}}\)
Bài 3 trang 25 SGK Toán 11 tập 2 – Cánh Diều là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, đặc biệt là các yếu tố như đỉnh, trục đối xứng, và giao điểm với các trục tọa độ. Việc hiểu rõ các khái niệm này là nền tảng để giải quyết bài toán một cách chính xác và hiệu quả.
Bài 3 thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai, vẽ đồ thị hàm số, và tìm các điểm đặc biệt trên đồ thị. Ngoài ra, bài tập còn có thể yêu cầu học sinh giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Để giải Bài 3 trang 25 SGK Toán 11 tập 2 – Cánh Diều, học sinh cần thực hiện các bước sau:
Giả sử hàm số cho là y = x2 - 4x + 3. Ta thực hiện các bước sau:
Khi vẽ đồ thị hàm số, cần chú ý đến dấu của hệ số a để xác định chiều mở của parabol (lên trên nếu a > 0, xuống dưới nếu a < 0). Ngoài ra, cần kiểm tra lại các bước tính toán để đảm bảo tính chính xác của kết quả.
Việc giải Bài 3 trang 25 SGK Toán 11 tập 2 – Cánh Diều không chỉ giúp học sinh củng cố kiến thức về hàm số bậc hai mà còn rèn luyện kỹ năng giải bài tập và tư duy logic. Những kiến thức này có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của toán học và khoa học tự nhiên.
Để nâng cao khả năng giải bài tập, học sinh có thể luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc tự giải bài tập và kiểm tra đáp án sẽ giúp học sinh nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Bài 3 trang 25 SGK Toán 11 tập 2 – Cánh Diều là một bài tập quan trọng, đòi hỏi học sinh phải nắm vững kiến thức về hàm số bậc hai và áp dụng các phương pháp giải bài tập một cách linh hoạt. Hy vọng với lời giải chi tiết và phân tích chuyên sâu trên đây, các em học sinh sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.
| Hệ số | Giá trị |
|---|---|
| a | 1 |
| b | -4 |
| c | 3 |