Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 43, 44 SGK Toán 11 tập 2 - Cánh Diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập trong mục 2 tập trung vào các kiến thức quan trọng của chương trình Toán 11, đòi hỏi các em phải có sự hiểu biết sâu sắc về lý thuyết và kỹ năng vận dụng linh hoạt.
Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

Phương pháp giải:
Dựa vào hàm lôgarit đã học rồi thay số
Lời giải chi tiết:
Cho hai ví dụ về hàm số lôgarit
Phương pháp giải:
Dựa vào định nghĩa hàm số lôgarit để xác định
Lời giải chi tiết:
\({\log _3}x;\,\,{\log _5}\left( {x + 2} \right)\)
Cho hàm số lôgarit \(y = {\log _2}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
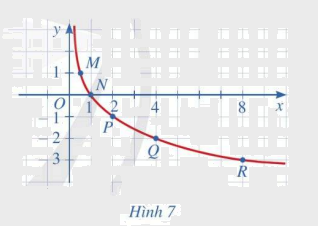
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _2}x\) như hình bên.

c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _2}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _2}x\), nêu nhận xét về:
Phương pháp giải:
Áp dụng kiến thức đã học về giới hạn và lôgarit để trả lời câu hỏi
Lời giải chi tiết:
a) \(y = {\log _2}x\)

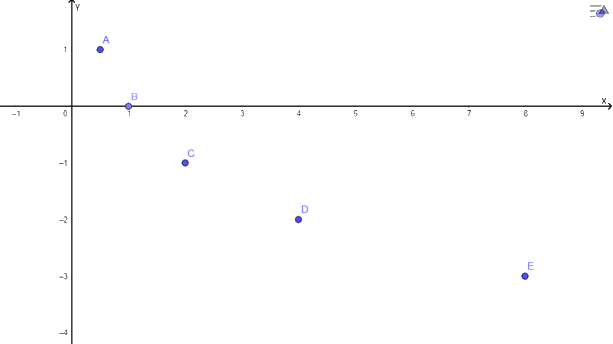
b, Biểu diễn các điểm ở câu a:
c, Tọa độ giao điểm của đồ thị hàm số với trục hoành \(y = {\log _2}x\)là (1;0)
Đồ thị hàm số đó không cắt trục tung.
d, \(\mathop {\mathop {\lim }\limits_{x \to {0^ + }} ({{\log }_2}x)}\limits_{} = 0;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_2}x)}\limits_{} = + \infty \)
Hàm số \(y = {\log _2}x\) đồng biến trên toàn \((0; + \infty )\)
Bảng biến thiên của hàm số:

Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.

c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\), nêu nhận xét về:
Phương pháp giải:
Áp dụng kiến thức đã học về giới hạn và lũy thừa để trả lời câu hỏi
Lời giải chi tiết:
a) \(y = {\log _{\frac{1}{2}}}x\)

b, Biểu diễn các điểm ở câu a:

c, Tọa độ giao điểm của đồ thị hàm số với trục hoành \(y = {\log _{\frac{1}{2}}}x\)là (1;0)
Đồ thị hàm số đó không cắt trục tung
c) \(\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = 0;\,\,\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = - \infty \)
Hàm số \(y = {\log _{\frac{1}{2}}}x\) nghịch biến trên toàn \((0; + \infty )\)
Bảng biến thiên của hàm số:

Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {\log _{\frac{1}{3}}}x\)
Phương pháp giải:
Dựa vào bảng biến thiên và đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) để làm
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{3}}}x = 0;\,\,\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{3}}}x = - \infty \)
Hàm số \(y = {\log _{\frac{1}{3}}}x\) nghịch biến trên toàn \((0; + \infty )\)
Bảng biến thiên của hàm số:

Mục 2 của SGK Toán 11 tập 2 - Cánh Diều thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các tính chất và ứng dụng của các phép biến hình này là vô cùng quan trọng để giải quyết các bài toán hình học một cách hiệu quả.
Phép tịnh tiến là phép biến hình di chuyển mỗi điểm trong mặt phẳng một khoảng không đổi theo một hướng xác định. Để giải các bài toán liên quan đến phép tịnh tiến, cần xác định vector tịnh tiến và áp dụng công thức biến đổi tọa độ.
Phép quay là phép biến hình biến mỗi điểm trong mặt phẳng thành một điểm khác sao cho khoảng cách từ điểm đó đến một điểm cố định (tâm quay) không đổi, và góc giữa hai đoạn thẳng nối tâm quay với điểm ban đầu và điểm sau khi quay là một góc cố định (góc quay).
Phép đối xứng trục là phép biến hình biến mỗi điểm trong mặt phẳng thành một điểm khác sao cho đường thẳng nối hai điểm đó vuông góc với một đường thẳng cố định (trục đối xứng) và trung điểm của đoạn thẳng nối hai điểm nằm trên trục đối xứng.
Phép đối xứng tâm là phép biến hình biến mỗi điểm trong mặt phẳng thành một điểm khác sao cho trung điểm của đoạn thẳng nối hai điểm là một điểm cố định (tâm đối xứng).
Để giải các bài tập trong mục 2 trang 43, 44 SGK Toán 11 tập 2 - Cánh Diều, các em cần:
Ví dụ, bài tập 1 trang 43 yêu cầu tìm ảnh của điểm A(1; 2) qua phép tịnh tiến theo vector v = (3; -1). Ta áp dụng công thức M'(x + vx; y + vy) để tìm được A'(1 + 3; 2 - 1) = A'(4; 1).
Để nắm vững kiến thức về các phép biến hình, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Ngoài ra, việc tìm hiểu các ứng dụng thực tế của các phép biến hình trong các lĩnh vực khác nhau cũng sẽ giúp các em hiểu sâu hơn về tầm quan trọng của kiến thức này.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin giải các bài tập mục 2 trang 43, 44 SGK Toán 11 tập 2 - Cánh Diều. Chúc các em học tập tốt!